Page 103 - Vol.33

Tech
Notes
技術專文

Jardine為此提出方法，估算單位 備設定未達最佳化，以及建造安裝
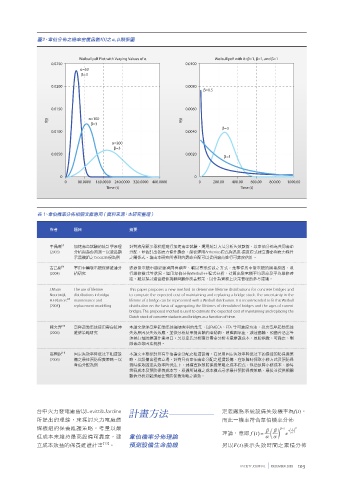
圖1、典型的浴缸失效率曲線 圖2、韋伯分佈之機率密度函數f(t)之α,β關係圖
時間下最佳保養維護成本，進而推 缺陷導致系統可靠度低而呈高失效
估如何以最小預防保養成本來維持 率狀態。然而隨著時間增加，廠務
設備可靠度 [2,3] 。除了準確預測系 系統工程師不斷進行系統改良、更 除錯期 平穩期 老化期 Weibull pdf Plot with Varying Values of α Weibull pdf with 0<β<1, β=1, and β>1
0.0250 0.0100
統設備生命曲線找出保養維護最適 換、校正及系統間的磨合使失效率 α=50
當時間點外，如何結合韋伯可靠度 會隨時間降低，而趨於低失效率穩 失效率 β=3
機率理論與Levitt & Jardine最小 定狀態。
0.0200 0.0080
保養維護成本方法？如何讓保養維 β=0.5
護的時間選擇與花費成本都達最佳 平穩期(Useful Life Period)
化？本文為此提出一套設備保養維 時間 0.0150 0.0060
經建廠初期後，系統逐漸穩定，各
護Model，並且以實際的ATRS資
設備間也調整磨合至完好的狀態， f(t) α=100 f(t)
料，來佐證本文所提出之最佳保養 β=3
此時期的失效率最低且位於設備壽 β=3
Model適用於廠務設備。 0.0100 0.0040
命浴缸曲線的中間位置，此時其失
效原因主要來自於意外失效，如地 的參數變化，所形成的機率密度函 α=200
β=3
震、震動、颱風、碰撞、異常溫度 數圖形具有多樣變化的特性，能以 0.0050 0.0020
變化或人員疏失所引起而產生系統 不同的分配參數組合來表示出品質 β=1
文獻探討 失效。此階段執行適當的保養維 資料的所有可能分布情況，藉以了

護，如日常點檢以及週期性預防保 解設備的可靠度，同時也已經有許 0 0
養，能延長此時期有效減緩設備老 0 80.0000 160.0000 240.0000 320.0000 400.0000 0 200.00 400.00 600.00 800.00 1000.00
可靠度理論 多跨領域的成功應用案例，如 表1 Time (t) Time (t)
化速度，進而延長設備壽命以減少 所示。
可靠度是一種量測系統性能的品質 故障發生。
衡量指標，大部分的系統隨著時間
增加，系統可靠度會逐漸下降，因 老化期(Wear-out Period) 設備保養維護方式與成本 表 1、韋伯機率分佈相關文獻應用 ( 資料來源：本研究整理 )
此必須施以適當的維護保養工作，
任何的設備一定有其壽命，此時期 Lie and Chun [12] 將設備之保養維護
以維持系統的正常運轉。現行系統 作者 題目 摘要
開始進入性能劣化，主要原因為
設備可靠度的定義是由美國國防部 方式分為預防保養維護(Preventive
「自然劣化」，如同材料疲乏、環
可靠度顧問小組進行相關研究所得 Maintenance -PM)與修正保養維護 李佩熹 [7] 加速壽命試驗的統計學原理 針對液晶顯示器模組進行加速壽命試驗，運用統計方法分析失效數據，以韋伯分佈為共同壽命
境影響磨耗、腐蝕等老化現象以及 (2003) 分析與壽命預測－以液晶顯 分配，並估計出各應力條件壽命，最後運用Arrhenius模式與溫度-濕度模式建立壽命與應力條件
到的結論，並定義可靠度是指一系 (Corrective Maintenance -CM)，
「人為劣化」，如不當操作或維護 示器模組之Crosstalk現為例 之關係式。藉由本研究所得到的壽命分配可以提供廠商進行可靠度估計。
統、設備或元件於既定的時間內， 為了預估出設備保養維護期望總成
不當等因素所引起，設備失效率隨 [3] 古昌彬 [8] 軍用車輛發電機保修維護分 透過發電機申撥紀錄與問卷調查、輔以專家訪談之方式，蒐整悍馬車發電機的損壞原因、現
在指定的操作條件(環境)，執行特 本，Jardine 為此計算理論基礎：
時間增加而快速遞增，位於浴缸曲 (2004) 析研究 行維修模式等狀況。運用韋伯分佈Weibull++程式分析、計算出發電機平均壽命及平均維修時
定的性能或功能，成功達成工作目 保養維護期望總成本 距。藉以探討適當維修規劃與翻修改善對策，以作為實務上決策管理的參考建議。
線的右方，失效率呈快速上升的狀
標的機率(=100%-失效率)。以上定
態。 J.M.van The use of lifetime This paper proposes a new method to determine lifetime distributions for concrete bridges and
義說明可靠度所包含之四項重點： Noortwijk, distributions in bridge to compute the expected cost of maintaining and replacing a bridge stock. The uncertainty in the
操作條件、操作時間、功能及機率 內維持穩定運轉 H.E.Klatterc [9] maintenance and lifetime of a bridge can be represented with a Weibull distribution. It is recommended to fit this Weibull
為設備在時間t p
C p
(2004) replacement modelling distribution on the basis of aggregating the lifetimes of demolished bridges and the ages of current
[4]
。因此可靠度可視為一種用機率 韋伯機率分佈 之預防保養總成本；C f 為故障更換 bridges. The proposed method is used to estimate the expected cost of maintaining and replacing the
來描述系統、設備或元件品質水準 內 Dutch stock of concrete viaducts and bridges as a function of time.
失效機率密度函數f(t)常用的有 平均成本；R(t p )為設備在時間t p
的指標。 內 陳文秀 [10] 空壓起動馬達使用壽命延伸 本論文透過空壓起動馬達損壞資料的蒐集，以FMECA、FTA 等可靠度方法，找出空壓起動馬達
常態分佈、對數常態分佈、指數 的可靠度；h(t p )為設備在時間t p (2006) 維修策略研究 失效原因及失效效應，並依分析結果提出軸向滑動閥、噴嘴閥承座、減速齒輪、預齒合活塞等
分佈、韋伯分佈。其中最為廣泛 的失效率。 須執行預防維護作業項目。另以韋氏分析獲得壽命分析考量維護成本、風險指數、可靠度、剩
餘壽命等因素規劃。
應用的就是韋伯機率分佈(Weibull Levitt 提出設備在其壽命週期內需
[2]
設備失效模式—浴缸曲線
Probability Distribution Function) 要適當的操作與維護，才能使設備 高國欽 [11] 固定失效率降低法下租賃設 本論文主要探討具有韋伯壽命分配之租賃設備，在使用固定失效率降低法下的最佳預防保養策
浴缸曲線也稱為標準的失效率曲 [6] ： 的功能保持正常運轉狀態，在其運 (2006) 備之最佳預防保養策略－以 略。以設備出租者立場，針對具有韋伯壽命分配之租賃設備，在故障時採取小修方式及預防保
線，系統設備之失效率會隨著時間 韋伯分配為例 養時採取固定失效率降低法下，建構實施預防保養策略之成本模式，包括故障小修成本、逾時
轉過程對它進行保養將延緩老化速 懲罰成本及預防保養成本等，根據所建構之成本模式尋求最佳預防保養策略，最後並提供相關
增加而變化，大致可分為三個時期 數值分析以驗證最佳預防保養策略之績效。
度，若對它進行修理或更換將可提
來討論，如 圖1所示。
高系統可靠度，但相對所需花費維
α為韋伯分佈之尺度參數，可衡量 護成本較高，其關係如 圖3所示。
除錯期 (Early Life Period) 存活壽命，當α增減時，分佈即從
圖中橫座標為保養維護次數，PM
中心點變高瘦或變矮胖。β為韋伯
此時期發生於設備壽命初期，該區 保養次數越多成本呈線性遞增，而 台中火力發電廠曾以Levitt&Jardine 計畫方法 定義廠務系統設備失效機率為f(t)，
分佈之形狀參數，決定分佈的形
間系統設備呈高失效率快速遞減狀 CM故障成本遞減，因此要找出最 所提出的理論，來探討火力電廠燃 而此一機率符合韋伯機率分佈
狀，如 圖2所示。
態，建廠初期系統設備剛建置完 適合之維護次數使總維護成本最 煤機組的保養維護策略，考量以最
理論，意即
成，開始投入運轉，因製程快速演 故韋伯分佈是應用最廣的失效機率 低，為規劃設備維護策略重要課 低成本來維持最高設備可靠度，建 韋伯機率分佈理論
進而系統設計缺乏經驗或各系統設 分配，主要的原因在於韋伯分佈中 題。 立成本效益的保養維護計畫 [13] 。 預測設備生命曲線 另以F(t)表示失效時間之累積分佈
102 FACILITY JOURNAL DECEMBER 2018 103