Page 92 - Vol.34

Tech
Notes
技術專文

析師Doug Laney首先在其發表的
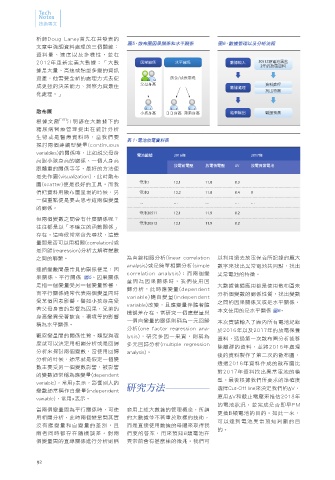
圖5、散布圖因果關係和水平關係 圖6、數據管理以及分析流程
文章中強調資料處理的三個關鍵：
資料量、速度以及多樣性，並在
2012年重新定義大數據：「大數 因果關係 水平關係 數據輸入 30512顆電池涵蓋
2年的放電資料
據是大量、高速或類型多變的資訊
資產，他需要全新的處理方式去促 飲食/成長環境
成更強的決策能力、洞察力與最佳 父母身高 數據處理 資料處理
找出特徵
化處理。」

散布圖 小孩身高 哥哥身高 弟弟身高 結果輸出 驗證預測

根據文獻 [15] 江明諺在大數據下的
糖尿病醫療管理提出在統計分析
生物或是醫療資料時，當我們要
表 1、電池放電資料表
探討兩個連續型變量(continuous
variables)的關係時，比如說父母身
電池編號 2016年 2017年
高跟小孩身高的關係、一個人身高
放電前電壓 放電後電壓 ∆V 放電異常電池
跟體重的關係等等，最好的方法便
是先作圖(visualization)，此時散布
圖(scatter)便是很好的工具。而我 電池1 12.1 11.8 0.3
們把資料用散布圖呈現的時候，另 電池2 12.2 11.8 0.4 V
一個重點便是要去思考這兩個變量
… … … … …
的關係。
電池30511 12.1 11.9 0.2
但兩個變數之間會有什麼關係呢？
電池30512 12.1 11.9 0.2
往往都是以「不確定的函數關係」
存在。這時候常常會先尋找，這變
量間是否可以用相關(correlation)或
是回歸(regression)分析去解釋變數
之間的聯繫。 為直線相關分析(linear correlation 以利用過去放電保養所記錄的龐大
analysis)或是簡單相關分析(simple 數字來找出異常電池共同點，找出
連續變數間最常見的關係便是：因
correlation analysis)；而兩個變 異常電池的特徵。
果關係、平行關係 圖5。因果關係
量間為因果關係時，我們使用回
是指一個變量受另一個變量影響， 大數據普遍應用都是使用散布圖來
歸分析，此時應變量(dependent
而平行關係通常代表兩個變量同時 分析個變數的關係性質，找出變數
variable)隨自變量(independent
受某個因素影響。譬如小孩身高受 之間的因果關係又或是水平關係，
variable)改變，且應變量伴隨者隨
著父母身高的影響為因果，兄弟的 本文使用的是水平關係 圖6 。
機誤差存在，當研究一個應變量與
身高變異受著飲食、環境等的影響
一個自變量的關係則稱為一元回歸 本次實驗輸入了廠內所有電池紀錄
稱為水平關係。
分析(one factor regression ana- 於2016年以及2017年的放電保養
觀察變量間的關係性質、類型與程 lysis)，研究多因一果實，則稱為 資料，透過第一次散布圖分析後移
度就可以決定用相關分析或是回歸 多元回歸分析(multiple regression
除離群的資料，並將2016年處理
分析來探討兩個變數，當使用回歸 analysis)。
後的資料製作了第二次的散布圖，
分析的時候，通常就是假定一個變
透過2016年資料作成的散布圖比
數主要受另一個變數影響，被影響
對2017年資料找出異常電池的模
的變數通常稱為應變量(dependent
型。最後根據我們所要求的準確度
variable)，常用y表示，影響別人的 研究方法
變數通常稱作自變量(independent 選擇Cut-Off line來決定我們的∆V，
應用∆V和截止電壓來推估2018年
variable)，常用x表示。
的電池狀況，並完成是否即早PM
當兩個變量間為平行關係時，可使 套用上述大數據的管理概念，所謂
更換B類電池的目的。如此一來，
用相關分析，此時兩個變量間其實 的大數據並不著重於取樣的技術，
可以達到電池異常預知判斷的目
沒有應變量和自變量的差別，且 而是直接使用數據的母體來取得我
的。
兩者同時都存在隨機誤差。對兩 們要的答案，用來預知B類電池在
個變量間的直線關係進行分析則稱 異常前會有甚麼樣的徵兆。我們可

92