Page 84 - Vol.35

Tech
Notes
技術專文

圖3、冰機12度迴路平均負載與系統冷凍噸二階回歸 圖5、冰機模型學習曲線：（上列）5C/12C耗電預測；（下列）5C/12C負載預測

100 120000 20000
Training 18000 Training
90 12C RT VS平均負載 100000 Cross-validation Cross-validation
y = 7E-07x - 0.0054x + 58.515 y = 4E-07x - 0.0031x + 50.92 y = 3E-07x - 0.003x + 51.417 16000
2
2
2
y = 3E-07x - 0.0024x + 45.748
2
2
80 y = 7E-07x - 0.0036x + 51.477 y = 6E-07x - 0.0054x + 60.175 y=3E-07x -0.004x+57.195 80000 14000
2
2
y = 5E-06x - 0.0057x + 233.54
2
y=3E-07x -0.0025x+47.846 12000
2
70 Mean Squared Error 60000 Mean Squared Error 10000
2
y = 1E-07x - 0.0003x + 26.079
60 40000 8000
6000
50 20000
4000
40 0 2000
5000 6000 7000 8000 9000 10000 11000 12000 13000 14000 15000 16000 17000 1000 1500 2000 2500 3000 3500 4000 4500 5000 5500 1000 1500 2000 2500 3000 3500 4000 4500 5000 5500
Training examples Training examples
6 sets 7 sets 8 sets 9 sets 10 sets 11 sets 12 sets 13 sets 14 sets 15 sets
45 16
40 Training 14 Training
Cross-validation Cross-validation
35 12
下負載。相較於方法一更加直覺， 30 10
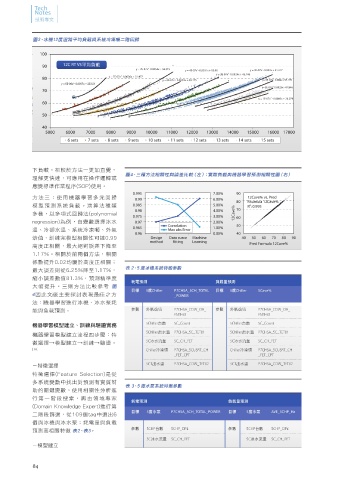
圖4、三種方法相關性與誤差比較（左）；實際負載與機器學習預測相關性圖（右） 25
理解更快速，可應用在操作運轉或 Mean Squared Error Mean Squared Error 8
應變標準作業程序(SOP)使用。 20 6
0.995 7.00% 90 15
方法三：使用機器學習多元回歸 0.99 6.00% 80 12Cave% vs. Pred 10 4
Foumula 12Cave%
模型預測系統負載。演算法種類 0.985 5.00% R : 0.995 5 2
2
0.98 4.00% 70
多樣，以多項式回歸法(polynomial 12Cave% 0
0.975 3.00% 60 0
regression)為例，自變數選擇冰水 0.97 Correlation 2.00% 50 1000 1500 2000 2500 3000 3500 4000 4500 5000 5500 1000 1500 2000 2500 3000 3500 4000 4500 5000 5500
溫、冷卻水溫、系統冷凍噸、外氣 0.965 Max abs Error 1.00% Training examples Training examples
0.96 0.00% 40
焓值，訓練完模型相關性可達0.99 Design Data curve Machine 40 50 60 70 80 90
method fitting Learning Pred Formula 12Cave%
高度正相關，最大絕對誤差下降至
1.17%。相關於前兩個方法，相關
機器學習模型我們以多項式迴歸 訓練完畢的機器學習模型如何套用
係數提升0.02均屬於高度正相關； 在系統運轉有幾個問題：模型可否
最大誤差則從6.25%降至1.17%， 表 2、5 度冰機系統特徵參數 (Polynomial Regression)為範例；一 根據梯度下降法，θ的最佳值是由
般式如下： 平台轉移？運算資源如何取用？資
縮小誤差數值81.3%，預測精準度 疊代求得，則
耗電預測 負載量預測 料流如何串接運作？
大幅提升。三則方法比較參考 圖
目標 5度Chiller P7CHSA_5CH_TOTAL 目標 5度Chiller 5Cave% 最簡單的方法是取用監控端電腦
4因此文後主要探討表現最佳之方 _POWER
Y 為預測值，在本研究中為冰 運算資源，但機器學習模型就必
法：機器學習進行冰機、冰水泵耗 其中 θ new 為新的參數向量， θ old
機與冰水泵的耗電量與負載； 為舊的參數向量， η 為學習速率 須簡單與具有平台轉移能力。例
能與負載預測。 參數 外氣焓值 P7CHSA_CDW_OA_ 參數 外氣焓值 P7CHSA_CDW_OA_
ENTH01 ENTH01 為特徵向量，即為 (Learning Rate)為自定義的值；疊 如python編譯訓練的隨機森林回
機器學習模型建立、訓練與驗證實務 5Chiller台數 5C_Count 5Chiller台數 5C_Count 特徵選擇後的變數； 代至收斂後，會得到最佳的θ，就 歸(Random Forest Regression)、
5Chiller出水溫 P7CHSA_5C_TET01 5Chiller出水溫 P7CHSA_5C_TET01 為參數向量，尋找最佳的參數向量 代表模型訓練完成。 深度類神經網路(DNN)運算邏輯較
機器學習模型建立流程四步驟：特
徵選擇→模型建立→訓練→驗證。 5C冰水流量 5C_CH_FET 5C冰水流量 5C_CH_FET 為訓練模型的關鍵。 複雜，平台轉移難度高，較適合
－模型驗證 雲端運算。多項式回歸(Polynomial
[16] Chiller冷凍頓 P7CHSA_5CUSRT_CH Chiller冷凍頓 P7CHSA_5CUSRT_CH
_FET_CPT _FET_CPT －模型訓練 機器學習的領域中會使用學習曲線 Regression)，模型簡單、訓練時
－特徵選擇 5CT出水溫 P7CHSA_CDW_TET02 5CT出水溫 P7CHSA_CDW_TET02 模型訓練的任務即為使用成本函數 (Learning Curve)來驗證一個已訓練 間短、運算量低，可輕便達到平
(Cost Function)與最佳化(Optimi- 完畢的模型。隨著訓練資料增加， 台間轉移。運轉上，便於系統負
特徵選擇(Feature Selection)是從
zation)找出最佳的一組參數向量 模型本身的訓練資料誤差(training 責人自主訓練機器學習模型調教
多系統變數中找出對預測有實質幫
表 3、5 度水泵系統特徵參數 係數 ，建立線上虛擬量測(Virtual
[5]
助的關鍵變數。使用相關性分析進 θ；一般線性迴歸模型成本函數使 erro r)與驗證資料誤差(Cro ss-
行第一階段搜索，再由領域專家 用MSE (mean-square error)： validation error)最終會收斂在一起 measurement)作為參考指標運轉。
耗電預測 負載量預測
(Domain Knowledge Expert)進行第 圖5、6、7、8；冰機耗電量預測精準 為進一步降低電腦運算負擔保持系
目標 5度水泵 P7CHSA_5CH_TOTAL_POWER 目標 5度水泵 AVE_5CHP_Hz 度約為48.88kW，冰水泵耗電量預
二階段篩選，從109個tag中選出6 統穩定度：由資料得知耗能(kW)與
當θ越佳時，J(θ)會越小；最佳化使 測精準度約為13.00kw；冰機負載 負載(Amp%)有顯著線性關係(歐姆
個與冰機與冰水泵；耗電量與負載
預測高相關特徵 表2、表3 。 參數 5CHP台數 5CHP_OP# 參數 5CHP台數 5CHP_OP# 用梯度下降法(Gradient-Descent)來 量預測精準度約為0.87%，冰水泵 定律P=I×V，V=4.16kV穩定供應
求得最佳的θ，首先先求J(θ)的雅可 負載量預測精準度約為0.53Hz 表 近常數)，機器學習僅訓練耗電預
5C冰水流量 5C_CH_FET 5C冰水流量 5C_CH_FET
－模型建立 比(Jacobi)為 4。 測、負載預測則用線性關係轉換，
84 FACILITY JOURNAL SEPTEMBER 2019 85