Page 52 - Vol.06

Tech
Notes
技術專文

1st Harmonic that there is modest variability between
1.0 individual measurements. For the second
Kerr
0.9 Galbrath & Barton third harmonics the increase of DLF with
0.8 Wheeler
Ohissen walking rate is slight, but there is a very
0.7
Rainer
0.6 Ellis significant scatter in the data.
DLF 0.5 Average
0.4 • Effective footfall impulse
0.3
There’s no buildup of vibration due
0.2
to successive footfalls, the measured
0.1
0.0 vibration-time history can be synthesized
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
Frequency (Hz) using the analytical expression for the
decay of vibration caused by an impulse.
2nd Harmonic
0.25 The initial velocity of a floor mode under
Kerr an impulsive action can be calculated
Galbrath & Barton
0.20
Wheeler by dividing the numerical value of the
Ohissen
0.15 Rainer impulse by the numerical value of the
Ellis
DLF Average modal mass. If the modal mass is 1.0 then
0.10 the initial velocity is numerically equal to
the applied impulse. This gives a method
0.05
to determine the ‘effective impulse’ of a
0.00 particular footfall force–time history.
0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0
Frequency (Hz)
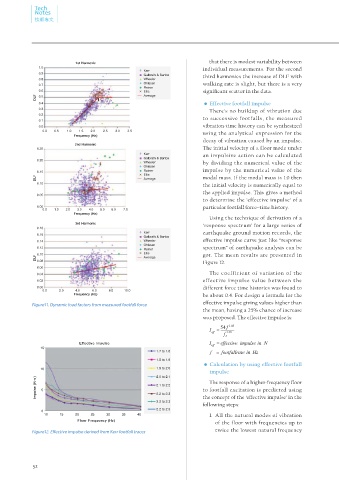
Using the technique of derivation of a
3rd Harmonic ‘response spectrum’ for a large series of
0.18
Kerr earthquake ground motion records, the
0.16
Galbrath & Barton
0.14 Wheeler effective impulse curve just like “response
Ohissen
0.12 spectrum” of earthquake analysis can be
Rainer
Ellis
DLF 0.10 Average got. The mean results are presented in
0.08
Figure 12.
0.06
0.04 The coefficient of variation of the
0.02 effective impulse value between the
0.00 different force time histories was found to
0.0 2.0 4.0 6.0 8.0 10.0
Frequency (Hz) be about 0.4. For design a formula for the
Figure11. Dynamic load factors from measured footfall force effective impulse giving values higher than
the mean, having a 25% chance of increase
was proposed. The effective impulse is:

Effective Impulse
15
1.7 to 1.8
1.8 to 1.9
• Calculation by using effective footfall
10 1.9 to 2.0
impulse
2.0 to 2.1
Impulse (N-s) 5 2.1 to 2.2 to footfall excitation is predicted using
The response of a higher-frequency floor
2.2 to 2.3
2.2 to 2.3 the concept of the ‘effective impulse’ in the
following steps:
0 2.2 to 2.3
10 15 20 25 30 35 40 1. All the natural modes of vibration
Floor Frequency (Hz)
of the floor with frequencies up to
Figure12. Effective impulse derived from Kerr footfall traces twice the lowest natural frequency

52