Page 18 - Vol.10
P. 18
Tech
Notes
技術專文
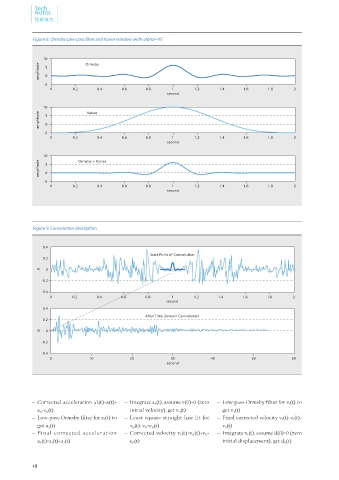
Figure 8. Ormsby Low-pass filter and Kaiser window (with alpha=10)
10 Ormsby
amplitude 5 0
-5
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
second
10 Kaiser
amplitude 5 0
-5
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
second
10 Ormsby + Kaiser
amplitude 5 0
-5
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
second
Figure 9. Convolution description
0.4
Start Point of Convolution
0.2
g 0
-0.2
-0.4
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
second
0.4
After Time Domain Convolution
0.2
g 0
-0.2
-0.4
0 10 20 30 40 50 60
second
– Corrected acceleration a1(t)=a(t)- – Integrate a 3 (t), assume v(0)=0 (zero – Low-pass Ormsby filter for v 1 (t) to
a 0 -c 0 (t) initial velocity), get v 0 (t) get v 2 (t)
– Low-pass Ormsby filter for a 1 (t) to – Least square straight line fit for – Final corrected velocity v 3 (t)=v 1 (t)-
get a 2 (t) v 0 (t): v 0 +e 0 (t) v 2 (t)
– Final corrected acceleration – Corrected velocity v 1 (t)=v 0 (t)-v 0 - – Integrate v 3 (t), assume d(0)=0 (zero
a 3 (t)=a 1 (t)-a 2 (t) e 0 (t) initial displacement), get d 0 (t)
18