Page 15 - Vol.10

time delays of interest.
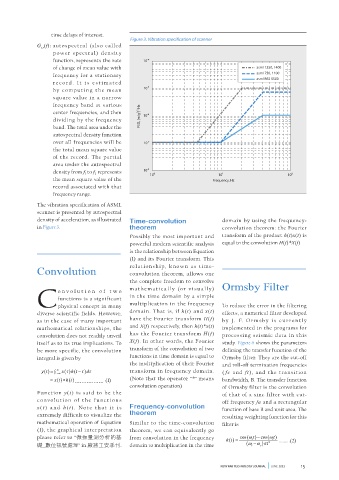
Figure 3. Vibration specification of scanner
G xx (f): autospectral (also called
power spectral) density
function, represents the rate 10
of change of mean value with asml 1250, 1400
frequency for a stationary asml 750, 1100
asml PAS 5500
r e c or d . It i s e st i m at e d
by comput i ng the mea n 10
square value in a narrow
frequency band at various
center frequencies, and then 10
dividing by the frequency PSD, (m/g ) Hz
band. The total area under the
autospectral density function
over all frequencies will be 10
the total mean square value
of the record. The partial
area under the autospectral
density from f 1 to f 2 represents 10
10 10 10
the mean square value of the Frequency, Hz
record associated with that
frequency range.
The vibration specification of ASML
scanner is presented by autospectral
density of acceleration, as illustrated Time-convolution domain by using the frequency-
in Figure 3. theorem convolution theorem: the Fourier
Possibly the most important and transform of the product h(t)x(t) is
powerful modern scientific analysis equal to the convolution H(f)*X(f)
is the relationship between Equation
(1) and its Fourier transform. This
relationsh ip, k now n as time-
Convolution convolution theorem, allows one
the complete freedom to convolve
m at he m at ica l ly (or v isua l ly) Ormsby Filter
on v o lu t i on o f t w o
functions is a significant in the time domain by a simple
Cphysical concept in many multiplication in the frequency To reduce the error in the filtering
diverse scientific fields. However, domain. That is, if h(t) and x(t) effects, a numerical filter developed
as in the case of many important have the Fourier transform H(f) by J. F. O r m sby i s cu r r e nt ly
mathematical relationships, the and X(f) respectively, then h(t)*x(t) implemented in the programs for
convolution does not readily unveil has the Fourier transform H(f) processing seismic data in this
itself as to its true implications. To X(f). In other words, the Fourier study. Figure 6 shows the parameters
be more specific, the convolution transform of the convolution of two defining the transfer function of the
integral is given by functions in time domain is equal to Ormsby filter. They are the cut-off
the multiplication of their Fourier and roll-off termination frequencies
y ( ) t = ∫ ∞ −∞ x ( ) ( htτ τ − )dτ transform in frequency domain. ( fc and ft), and the transition
= x ( ) t ∗ ht (Note that the operator “*” means bandwidth, B. The transfer function
( ) ................. (1)
convolution operation) of Ormsby filter is the convolution
Function y(t) is said to be the of that of a sinc filter with cut-
convolut ion of t he f u nct ions off frequency fa and a rectangular
x ( t ) a nd h ( t ) . Note t h at it i s Frequency-convolution function of base B and unit area. The
extremely difficult to visualize the theorem resulting weighting function for this
mathematical operation of Equation Similar to the time-convolution filter is
(1), the graphical interpretation theorem, we can equivalently go
please refer to “微振量測分析的基 from convolution in the frequency ht cos ( tω c ) cos− ( tω 2 t ) .........(2)
( ) =
) t
礎_數位訊號處理” in 廠務工安季刊. domain to multiplication in the time (ω − ωπ
c
t
NEW FAB TECHNOLOGY JOURNAL JUNE 2013 15