Page 16 - Vol.10

Tech
Notes
技術專文

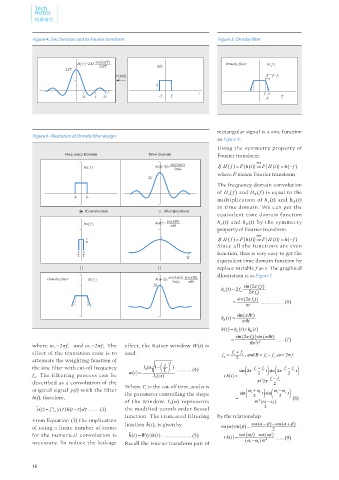
Figure 4. Sinc function and its Fourier transform Figure 5. Ormsby filter

H( f )=2AT sin(2πfT) h(t) Ormsby filter H( f )
2πfT
2AT
F{h(t)} B = ft - fc
A
f
1 1 3 t fc ft
2T T 2T -T T fa T

rectangular signal is a sinc function
Figure 6. Illustration of Ormsby filter design
as Figure 4.
Using the symmetry property of
Frequency Domain Time Domain Fourier transform:

sin(2πfat) then
( )}⇒
( )} h=
Ha( f ) ha(t)=2fa 2πfat If H ( ) f = F {h t F {H t ( f− )
where F means Fourier transform
2fa
The frequency domain convolution
of H a (f) and H B (f) is equal to the
-fa fa
multiplication of h a (t) and h B (t)
in time domain. We can get the
(Convolution) (Multipication)
equivalent time domain function
HB( f ) hB(t)= sin(πBt) h a (t) and h B (t) by the symmetry
πBt
property of Fourier transform.
then
( )} h=
( )}⇒
1 1 If H ( ) f = F {h t F {H t ( f− )
B
Since all the functions are even
B B
- 1 function, thus is very easy to get the
2 2
B
equivalent time domain function by
replace variable f as t. The graphical
=
=
Ormsby filter H( f ) h(t)=2fa sin(2πfat) sin(πBt) illustration is as Figure 7.
2πfat πBt
2fa sin (2 f tπ )
h a ( ) t = 2 f a 2 f t a a
π
= sin (2 f tπ a ) ................... (6)
t π
sin ( Btπ )
( ) =
ht π Bt
B
ht h a ( ) t × h B ( ) t
( ) =
sin (2 f tπ )sin ( Btπ )
= a 22 ...... (7)
π
where ω c =2πf c and ω t =2πf t . The effect, the Kaiser window W(t) is B t
effect of the transition zone is to used. f = a f + f t , and B = f t c , f ω − 2 f
π =
c
attenuate the weighting function of 2 2
t
(
the sinc filter with cut-off frequency I 0 (α 1− ( ) ) ............ (4) sin 2 π f + c f t t ) ( π f − t f c t )
T
sin 2
( ) =
c
( )
f a . The filtering process can be wt I α → ht 2 f − f 2
( ) =
0
described as a convolution of the t π 2 2 π t 2 c
original signal y(t) with the filter Where T c is the cut-off time, and α is sin ( ω c ω + t t ) ( ω t ω − c t )
sin
h(t); therefore, the parameter controlling the shape = 2 2 (8)
of the window. I 0 (α) represents t π 2 (ω t ω − c )
 y ( ) t = ∫ ∞ −∞ y ( ) ( htτ τ − )dτ .........(3) the modified zeroth order Bessel 2
function. The truncated filtering by the relationship:
From Equation (3) the implication  cos (α β − ) cos− (α β + )
ht
β
of using a finite number of terms function ( ), is given by sin ( )sinα ( ) = 2

( ) W t ht=
for the numerical convolution is ht ( ) ( ) ........................ (5) → ht cos ( tω c ) cos− ( tω t ) .......(9)
( ) =
) t
necessary. To reduce the leakage Recall the Fourier transform pair of (ω − ωπ 2
t
c
16