Page 22 - Vol.39

6
5
4
7
10
9
8
1
2
3
Tech
Notes
技術專文
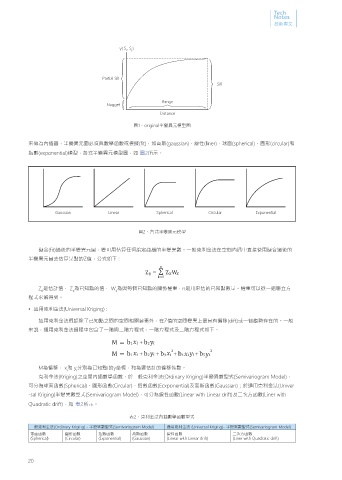
γ( S , S )
i
j
Partial Sill
Sill

Range
Nugget
Distance
圖1、original半變異元模型圖

來做為內插器，半變異元圖必須與數學函數或模擬(fit)，如高斯(gaussian)、線性(liner)、球面(spherical)、圓形(circular)和

指數(exponential)模型，各式半變異元模型圖，如 圖2所示。

Gaussian Linear Spherical Circular Exponential

圖2、各式半變異元模型

擬合(fit)過後的半變異元圖，變可用估算任何給定距離的半變異數。一般克利金法在空間內插中直接使用擬合過後的
半變異元圖去估算某點的Z值，公式如下 :
n
Z = ∑ Z W
0
k =0
Z 是估計值， Z 為已知點的值， W 為與每個已知點的關係權重，n是用來估的已知點數量。權重可以從一組聯立方
0 x x
程式求解得到。
• 通用克利金法(Universal Kriging) :

通用克利金法假設除了已知點之間的空間相關要素外，在Z值的空間變異上是具有偏移(dift)或一個趨勢存在的。一般
來說，通用克利金法過程中包含了一階與二階方程式，一階方程式及二階方程式如下。

M = b1 + b y
2
2 2
M = b1 + b y + b3 + b4 y +b5 y
2
M為偏移， x和 y分別為已知點i的y坐標，和為要估計的偏移係數。
i i
克利金法(Kriging)之空間內插數學函數，於一般克利金法(Ordinary Kriging)半變異數型式(Semivariogram Model)，
可分為球面函數(Spherical)、圓形函數(Circular)、指數函數(Ecxponential)及高斯函數(Gaussian)；於通用克利金法(Univer
-sal Kriging)半變異數型式(Semivariogram Model)，可分為線性函數(Linear with Linear drift)及二次方函數(Liner with
Quadratic drift)，如 表2所示。

表2、克利金法內插數學函數型式
一般克利金法(Ordinary Kriging) - 半變異數型式(Semivariogram Model) 通用克利金法 (Universal Kriging)- 半變異數型式(Semivariogram Model)
球面函數 圓形函數 指數函數 高斯函數 線性函數 二次方函數
(Spherical) (Circular) (Exponential) (Gaussian) (Linear with Linear drift) (Liner with Quadratic drift)

11 12 13 14 15 16 17 18 19 20

21 22 23 24 25 26 27 28 29 30

31 32 33 34 35 36 37 38 39 40

41 42 43 44 45 46 47 48 49 50