摘要

樓版勁度量測及分析
廠房的微振等級通常是由垂直向振動所控制,而垂直向振動則和樓版的勁度(stiffness)相關,有關樓版勁度的設計通常先用有限元素法(Finite Element Method)數值模擬求出其勁度,再配合結構體完成後之現場勁度量測以驗證數值模擬之準確性,本文主要介紹樓版勁度現場量測,從最基本的理論、量測的儀器、現場量測及分析,同時亦以實測結果說明並檢討結構之配置。
前言 Introduction
樓版的勁度(stiffness)控制著垂直向的變形及振動,一般的建築物除了某些運動場所如體育館、舞廳(如最近國外有某棟建築物因有氧舞蹈造成建築物產生共振)等需考慮振動外只要考慮變形量即可,然而半導體廠房對微振的要求相當高,對振動的控制也就相對重要,像scanner即對樓版的勁度有明確的規範。

公司的微振設計一向委託Colin Gordon Associates(以下簡稱CGA)設計,CGA先以有限元素法求得樓版勁度,再以他們的半經驗公式預估微振值,當廠房蓋好後則至現場以衝擊鎚配合加速度規進行勁度量測以驗證數值模擬之準確性,在國內部份則因為部份機台裝機前須對機台之混凝土基座確認其勁度是否符合機台規範,此部份之實驗大部分委由國內廠商進行實驗,但是經由多次和他們共同實驗或者藉由審視他們的測試報告發現,某些廠商並沒有基本的理論基礎,導致測試結果並不理想甚至有許多謬誤而不自知, 本文從最基礎的基本理論說明並介紹量測儀器及其原理,再從實際測試結果討論結構的配置,希望對以後廠房設計及現場測試有所幫助。
基本理論 Basic theory
單自由度具阻尼系統之激振響應
考慮單自由度系統如圖一所示,其運動方程式為:
圖一、單自由度系統
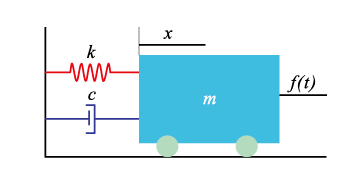
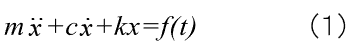
其中 mẍ 是慣性力inertia force, cẋ 是阻尼力damping force(energy dissipater),kх 是彈簧力或稱為回復力restoring force。
設激振力 f(t)=Foeiwt,則可設 x(t)=Xoeiwt 以求得穩態解(steady state solution),將 f(t)=Foeiwt 及 x(t)=Xoeiwt 代入運動方程式可得
(k-mw2+icw)Xoeiwt=Foeiwt,消去共同項可得

其中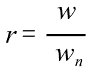
H(w) 稱為頻率響應函數 Frequency Response Function (FRF),其意義為每單位的輸入(本例中為激振力)有多少的輸出(本例中為位移),上式為複數型態,可以H(w)之大小|H(w)|及相位角φ改寫成

通用的頻率響應函數
依照量測輸出單位的不同(速度及加速度)會有不同的頻率響應函數,其名稱也各異。說明如下:
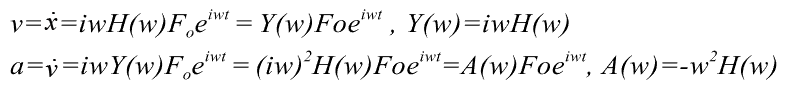
頻率響應函數的定義整理如表一所示。
|
Response |
Definition |
Name |
|---|---|---|
|
Displacement |
x | F = H (ω) |
Receptance |
|
Velocity |
v | F = Y(ω) = iω H(ω) |
Mobility |
|
Acceleration |
a | F = A(ω) = i ω Y(ω) = -ω 2H(ω) |
Accelerance |
其中receptance的倒數稱為dynamic stiffness動態勁度,其圖形在接近低頻處會成一水平線,此即為靜態勁度static stiffness。
由以上說明可知只要量得H(ω)、Y(ω)或A(ω)中的任一個,即可根據其相互間之關係式求出另兩個頻率響應函數。
由方程式(2),我們可由ω和ωn的關係觀察出一些現象:
● 當ω<<ωn,亦即r→0,此時方程式為彈簧常數k控制,亦即H(ω)≈1/k
● 當ω≈ωn,亦即r→1,此時方程式為阻尼c所控制,H(ω)≈1/icw
● 當ω>>ωn,此時方程式為質量m所控制,H(ω)≈1/(-mw2)
現已一質量m=4749.4kg,彈簧係數k=3x108n/m(此時ω=40Hz),阻尼c=375000之理想化單自由度系統為例分別繪出receptance、mobility、accelerance分別如圖二、三、四所示。由圖二之receptance可看出在低頻處為接近水平線,在自然頻率處形成一尖峰,往高頻處又逐漸形成斜直線。而圖三之mobility則在低頻及高頻處為接近斜率固定之直線,圖四之accelerance則為在低頻處為接近斜率固定之直線,在高頻處則為接近水平之直線。需注意在多自由度系統中因有多個模態(mode),其圖形變的比較複雜,不過在低頻的區域仍是如上述說明的狀況。
圖二、Receptance

圖三、Mobility
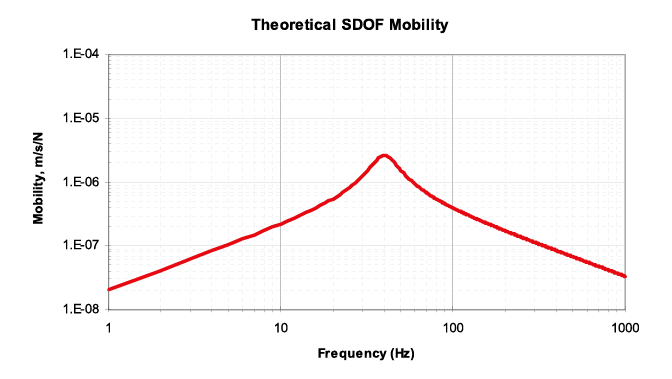
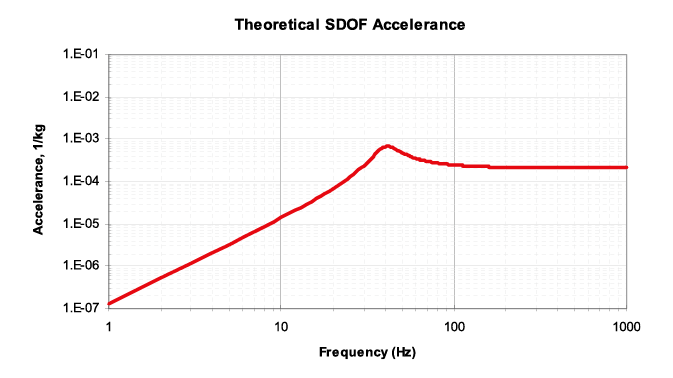
圖四、Accelerance
Coherence (一致性)
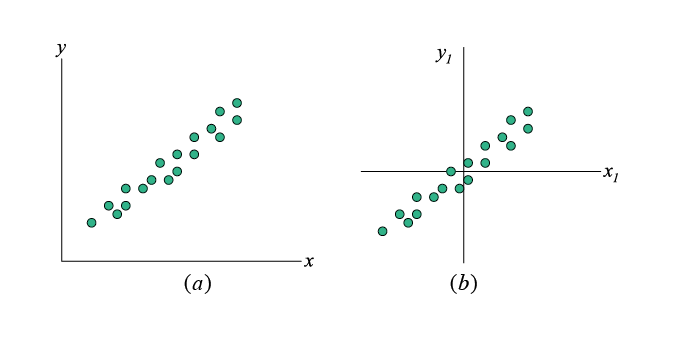
實驗時輸入(F)和輸出(x, v, a)的關聯性是判斷實驗成果可靠性的依據,亦即必須判斷此輸出反應是否是由此輸入所引起,而此判斷的基準就是coherence。首先由統計學的觀點來看相關correlation的概念,考慮如圖五(a)x, y的資料,透過下述線性關係將其轉換成如圖五(b)。
圖五、線性資料的轉換

則最佳的直線方程式可寫為

其中yp為y1的預估值,則其偏移量為
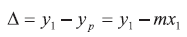
當然偏移量是越小越好,也就是將Δ2最小化,做法是利用數學上的期望值(expectation,其運算符號為E[x]),
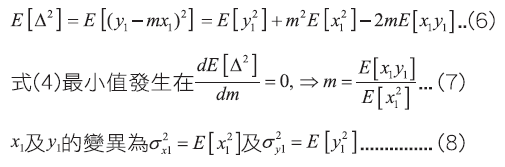
將式(4)(7)(8)代入(5)可得
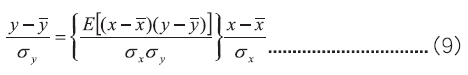
上式中大括弧內為正規化相關係數Pxy
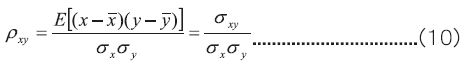
其中σxy稱為互相關係數(cross-correlation coefficient)
當pxy,則此資料為完全相關,pxy=0 則為完全不相關。正規化相關係數pxy是用來衡量資料x, y有多“類似”的參數。
應用式(10)的概念以及傅立葉變換和統計(或是機率)的理論(auto-correlation自相關,cross-correlation互相關等),取以頻率ω為變數之coherence函數y2(ω)
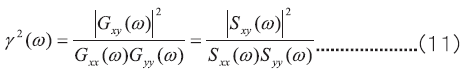
其中Sxx為均方頻譜密度(mean square spectral density)或稱為自頻譜密度(auto-spectral density),亦有人稱為功率頻譜密度(power spectral density), Sxy則為互頻譜密度(cross-spectral density),Gxx為單邊自頻譜密度(one-sided auto-spectral density)。
γ2(ω)的值永遠 ≦1,越接近1代表數據的一致性越好也就是可靠性越高,然而在自然頻率附近,因為共振的影響,其coherence會較差。
量測儀器及其原理 Measuring instruments and principles
量測儀器
FRF簡單的說明就是output/input,亦即在每單位力作用下受測體有多少反應,而這反應可以是位移、速度或加速度。其中的input在實際應用上有多種方式,包括產生單頻頻率振源的激振器,產生複頻頻率的衝擊鎚或快速釋放法等,其中最方便的是衝擊鎚(impact hammer),因其攜帶方便機動性強,衝擊鎚的型式有很多種,實際應用時需注意其使用限制及欲敲擊結構的特性選擇適當的衝擊鎚,像建築物這麼龐大的量體可以想像若欲用衝擊鎚進行實驗幾乎是不可能的。至於量測受測體反應的儀器仍以加速度規為主,然而加速度規之選擇卻關係到量測結果的優劣,後面章節將有較詳細之討論。
衝擊鎚的原理
如圖六所示,利用理想的單位力作用下其傅立葉變換為各頻率均等之水平線,亦即單位力衝擊下可激發複頻的反應,所謂理想的單位力是指作用力的作用時間趨近於0 (或者需符合衝擊函數δ,此屬廣義函數之定義,即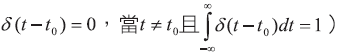 。
。
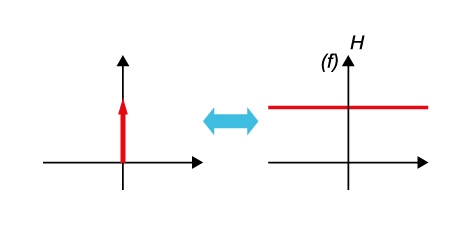
圖六、單位力的傅立葉轉換
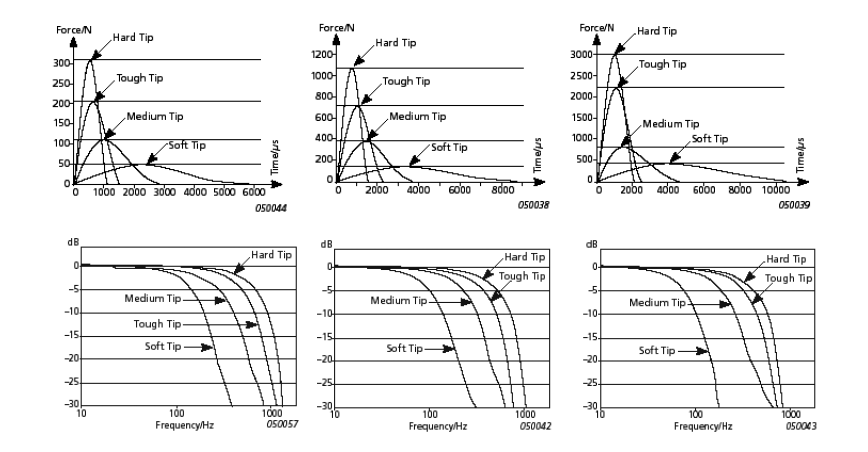
然而實際的應用中不可能產生此理想的力量,其在頻率域的延伸有其限制,如圖七、八所示,一般市售的衝擊鎚均會附上從軟到硬不同型式衝擊頭,圖八中可看出不同型式衝擊頭(以不同的顏色區分)之力量歷時之差異,越硬的衝擊頭其接觸時間越短,造成的力量越大,同時在頻率域的延伸也越寬;所以針對不同的受測體需依照受測體特性如頻寬範圍、力量大小等選擇適合的衝擊鎚設備,對樓版這種混凝土建築結構,其主要特徵是在低頻部份,實際測試時只要選取頻寬範圍最小之軟性衝擊頭即可。
圖七、幾種不同型式的衝擊鎚

圖八、不同型式衝擊鎚頭之力量歷時及相對應之頻譜
樓版結構的型式 Structure type
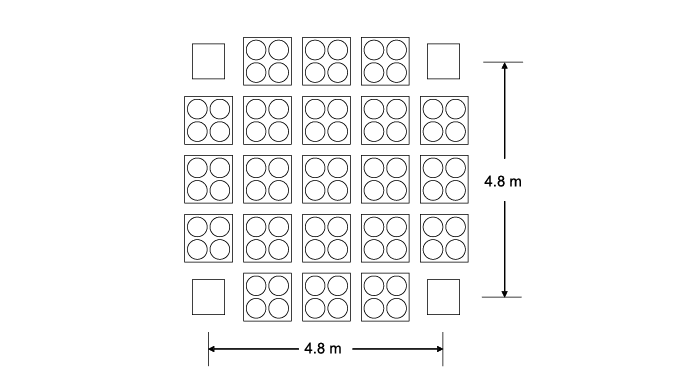
半導體生產廠房中隨著製程的不同對微振也有不同的需求,相對的廠房設計時也就針對製程而有不同的設計規範,如HPM 3F和F15 CUP 3F及4F之SUP區,其製程微振規範分別只需符合VC-B(vibration curve B)=1000μin/s及VC-A(vibration curve B)=2000μin/s,此時只要傳統的樓板結構即可符合要求。傳統的樓版結構主要是由樑、柱系統支撐樓版所構成,其中和柱相接的樑稱為大樑(girder),而和大樑相接的樑稱為小樑(beam),其配置通常依設計載重需求而異;但對半導體廠房中對振動最敏感之設備如scanner, CD-SEM, E-beam writer而言則另需再考慮較嚴格之微振動之需求,傳統的樓版結構已無法滿足,必須使用格子樑(waffle slab)樓版搭配較小的柱距(本例為4.8m)如圖九及圖十所示,waffle slab可提供較高的樓版勁度;公司自F6以後之新建廠房在ballroom全部採用此型式之waffle slab,在12吋廠中則把圖九中平板厚度由15cm增加至20cm,總樑深也由95cm增至100cm。其他如F8樓版則為跨距4.2m×4.2m,厚度60cm開圓孔(直徑35cm)之cheese type樓版,而F3E樓版則為跨距3.6m×3.6m,厚度40cm開孔甚大為長方形(分別為100cm×40cm及85cm×40cm)之樓版。
圖九、waffle slab 剖面

圖十、waffle slab 平面
測試廠房其微振規範大部分為VC-A或VC-B,通常不會為測試廠房獨立蓋一棟建築物,此時常在一般辦公棟的其中某個樓層做局部結構加強,很多辦公棟之結構是鋼結構,因為鋼柱之勁度及阻尼較小,此時就要特別注意樓層高度的影響,美國鋼構造協會AISC在其刊物 “AISC Design Guide 11: Floor Vibrations Due to Human Activity”所提出之公式中即需將樓層高度考慮進去,在實際的測試中也發現樓層高度的因素影響非常大。
實測案例及討論 Case and discussion
測試注意事項
實際測試時最好在結構體完成且廠務轉動設備尚未開始運轉前-亦即背景振動值越小越好,尤其對比較軟的非格子樑的樓板系統,此時測試的效果會最好,因為轉動設備所引起的振動會和hammer敲擊所引發的振動混雜在一起而影響分析的結果。
測試時最好將加速度規以適當方式固定在樓板上,若使用尺寸較小的加速度規,可使用蜜蠟將其固定在樓版上,否則則可先在地板上貼上膠帶,再利用雙面膠帶將加速度規固定在已黏貼之膠帶上。
以hammer敲擊時理論上是越靠近加速度規越好,實務上的作法是距離約10公分左右;測試時須將加速度規的訊號放大倍數儘量放大(某些系統無法調整放大倍率)以將雜訊儘可能降低,但是敲擊過程中需隨時注意訊號強度包含hammer及加速度規是否超出範圍,若超出範圍則需調整敲擊力道或放大倍率。
實際測試案例
在格子樑部分,F15 L30層waffle slab為柱距4.8m×4.8m,樑深100cm,其測試結果如圖十一所示,F10 C/S為樑深95cm,柱距9.6m×4.8m之waffle slab,其測試結果如圖十二所示,F10B為樑深95cm,柱距4.8m×4.8m之waffle slab (和F6相同),其測試結果如圖十三所示。
圖十一、F15 Fab L30 量測結果
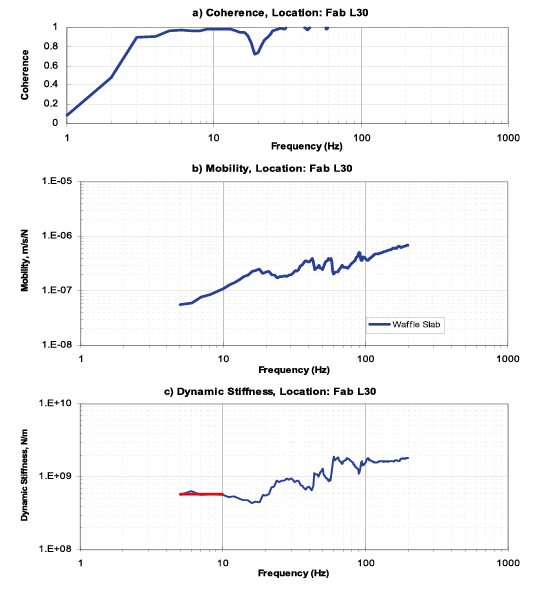
圖十二、F10 C/S L30 量測結果
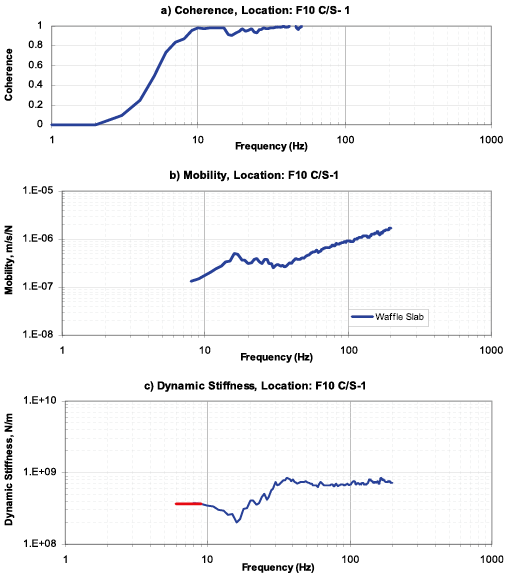
圖十三、F10B L30 量測結果
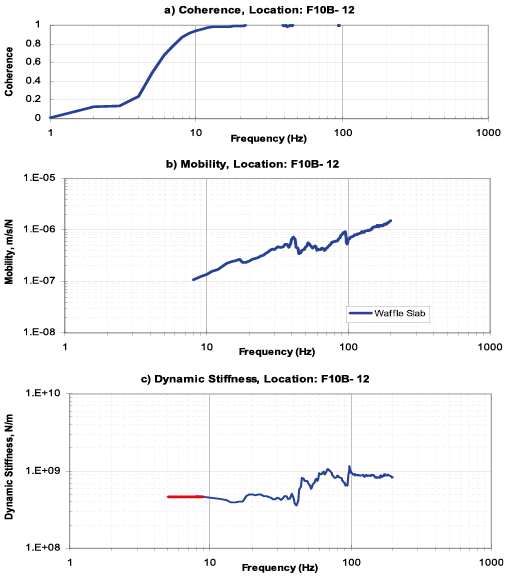
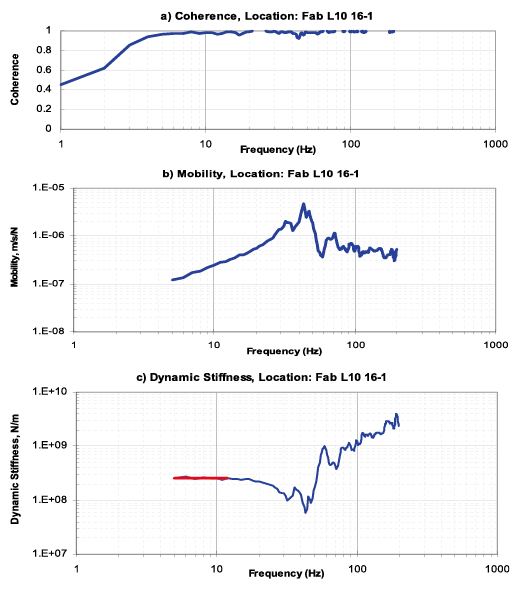
在非格子樑部分,圖十四至圖十七分別為F15 L10層、F15 CUP L30層、F15 L20層及F15 HPM L30層之測試結果,將測試結果整理如表二。
圖十四、F15 L10 量測結果
圖十五、F15 CUP L30 量測結果
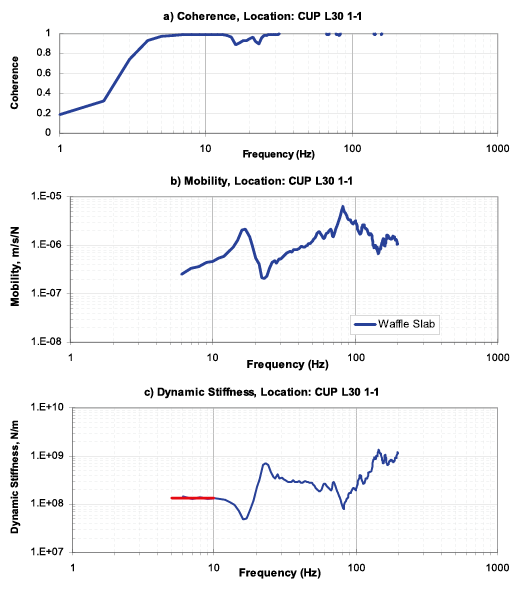
圖十六、F15 L20 量測結果
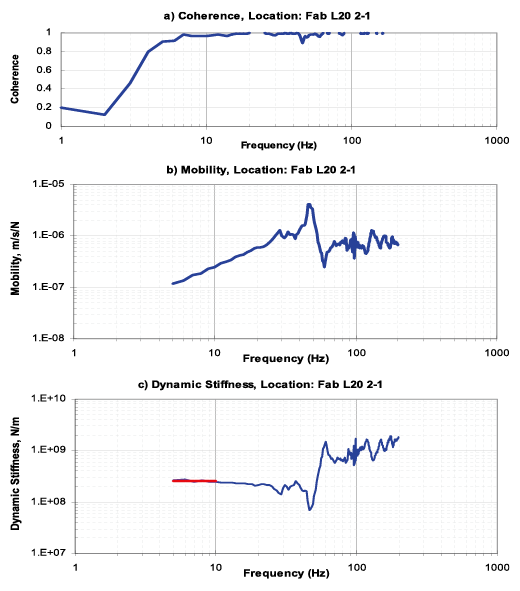
圖十七、F15 HPM L30 量測結果
|
位置 |
F15 L30 |
F10 C/S L30 |
F10B L30 |
F15 L10 |
F15CUP L30 |
F15 L20 |
F15HPM L30 |
|---|---|---|---|---|---|---|---|
|
結構型式 |
100cm深 格子樑 |
95cm深 格子樑 |
95cm深 格子樑 |
單向樑 |
雙向樑 |
單向樑 |
單向樑 |
|
柱距 |
4.8m×4.8m |
9.6m×4.8m |
4.8m×4.8m |
4.8m×4.8m |
9.6m×9.6m |
4.8m×4.8m |
9.6m×9.6m |
|
勁度 (N/m) |
5.8E8 |
3.8E8 |
4.5E8 |
2.6E8 |
1.34E8 |
2.6E8 |
2.1E8 |
測試結果討論
由測試結果可看出來在dynamic stiffness的圖形,在低頻區段均有趨近於水平線的理論特性,至於為何水平線無法延伸至6Hz以下,同時coherence在低頻段的值也比較差,這是因為低頻的振動需極大的能量方能激發,同時背景環境的振動主要以低頻為主,但是上述因素並不影響對靜態勁度(static stiffness)的判斷。
另外一個令人感到興趣的是同為柱距9.6m×9.6m的F15CUP L30及F15HPM L30,其中CUP為雙向樑配置,樑距為3.2m (圖十八),HPM則為單向樑配置,樑距為2.4m (圖十九);一般直覺會認為CUP之結構樓版勁度較HPM高,然而實測結果卻相反,微振顧問CGA之設計亦是CUP之微振值為2000μin/s,HPM為1000μin/s;當然有可能是CUP擺放許多大型之轉動設備如chiller及compressor等造成其振動值較高。然而其樓版勁度之差異卻讓我們重新思考結構配置,CUP之井字樑配置不僅成本較高且因小樑有許多交叉施工非常困難,結果其樓版勁度反而較差,此部份將再利用有限元素法數值模擬進一步探討以找出根本原因,對以後結構設計也有所幫助。
圖十八、F15 CUP 樓版結構平面圖

圖十九、F15 HPM 樓版結構平面圖

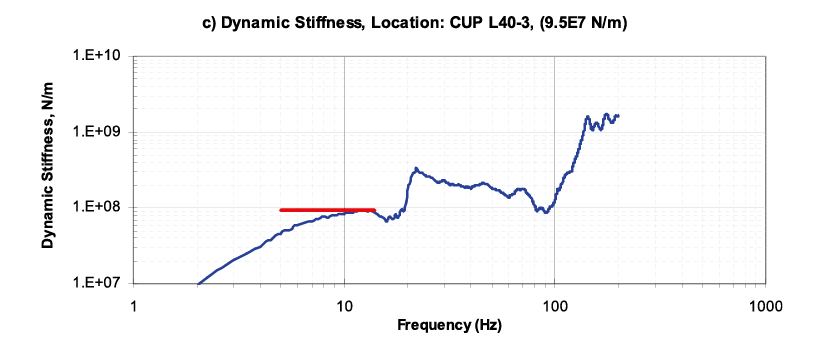
另外就是前面章節所提到的樓層高度的影響,CUP L30層及L40層之結構配置相同同為雙向樑結構,但是L40層樓版勁度(圖二十)為9.5E7 N/m,小於L30層樓版勁度1.34E8 N/m,實測結果證明樓層高度確實對樓版勁度有所影響。
圖二十、F15 CUP L40 樓版勁度
結論 Conclusion
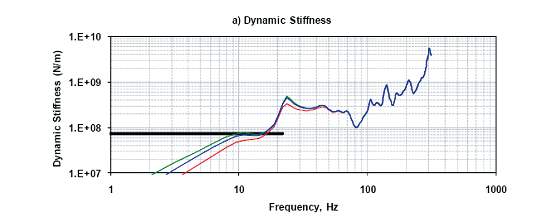
實務上有許多機會和微振顧問CGA一起做測試及量測,在F15的量測時,CGA使用和之前不同的加速度規(hammer相同),然而量測的品質卻大不如前;圖廿一及圖廿二分別是CGA和tsmc在同一位置之測試結果,其值分別是7.24E7(CGA)及1.34E8(tsmc),差異非常大,然而檢視CGA之圖廿一可發現其並無明顯之水平線,表示其在低頻段之結果並不可靠,他的勁度值可說是用猜出來的,由此可見慎選儀器的重要性。
圖廿一、CGA 所測試 CUP L30 樓版勁度
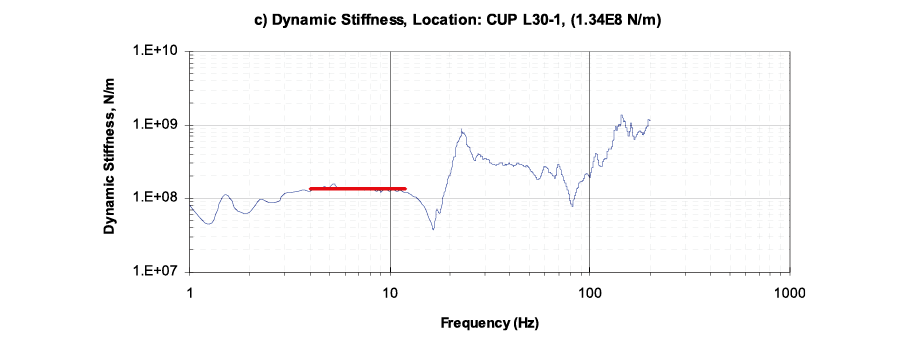
圖廿二、tsmc 所測試 CUP L30 樓版勁度
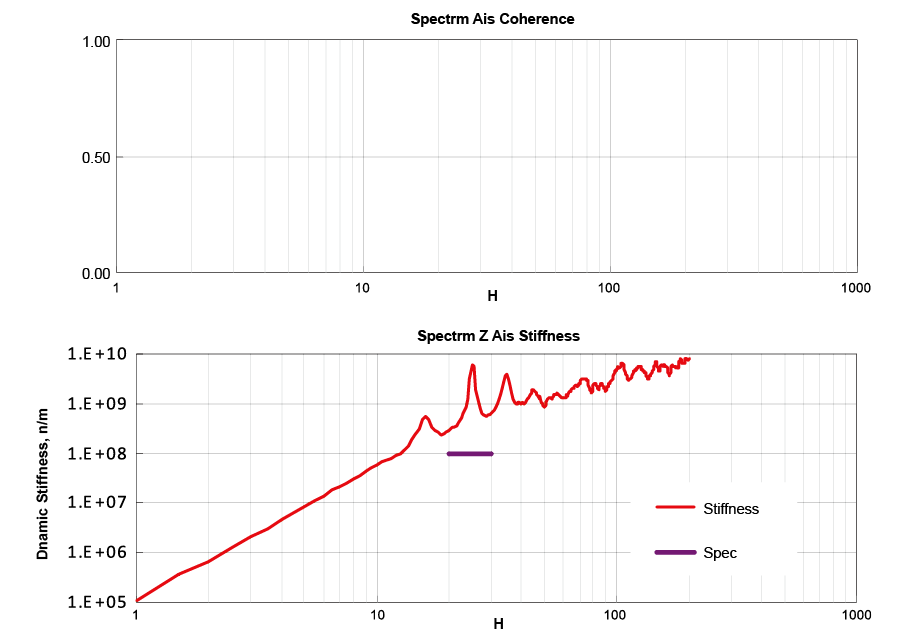
圖廿三為某家協力廠商之測試結果,其結果可說是錯的離譜,首先coherence不可能是完美的,再來dynamic stiffness找不到趨近於水平線的部份,同時spec.只標明在20至30Hz區間(asml規範只說明需符合1E8 N/m)亦是錯誤的觀念,此份報告從頭錯到尾,然而通常我們的sponsor卻是接受此報告的;顯然大部份的人包括實際作實驗的人對勁度測試的原理根本不瞭解,甚至有經驗的外籍顧問亦可能犯錯而不自知,希望本篇文章對以後需接觸勁度測試的人能有所幫助。
圖廿三、協力廠商之測試結果

留言(0)