摘要

不斷電系統電池異常即早維修保養判斷手法
Keywords / Uninterruptible Power Supply (UPS)4,Lead-acid Batteries,Early Detection4
各大晶圓廠廣泛使用不斷電系統(UPS)來預防不可預期的電壓降或短時間的電力中斷。電池則是UPS內部提供儲存能源唯一且重要的單元,因此電池可靠度以及健康狀況是一項非常重要的課題。我們透過電池放電檢測紀錄大量的資訊,利用這些大數據回歸,用以更有效地找出異常電池並推估即將異常的電池,即早規畫可預期的異常並及早改善,大大的提升UPS防禦台電電壓異常的可靠度,達到真正的「不斷電系統」。
前言
為了保證不斷電系統(Uninterrupted power system, UPS)能夠在電力壓降和短時間的電力中斷能夠有效的提供能量,讓用戶端達到供電不中斷的情況,時時刻刻保持電池的良好健康狀況是一件重要的課題。如何判斷一顆電池是否健康、是否需要更換新品,過去有許多文獻[9][10]來探討相關的議題。電池製造商[6][7]以及相關電池壽命探討資訊[13]也強調,電池使用達容量等級的80%時,會出現電池快速劣化的風險。此外,IEEE-1188也同樣有相關使用電池容量達80%時的電池更換建議內容。此手法分享給即將大批更換老化電池卻又無從下手的夥伴們。
電池更換我們一直沒有標準,電池年份到了,靠著經驗法則一批批的更換。並沒有一個數據告訴我們,那些風險高需要先更換,哪些風險低可堪延用。本文主要針對高年份的電池進行預測更換,預知你需要更換哪些即將異常的電池,並延長使用其餘堪用電池的年限。
放電及更換標準
目前廠內使用電池放電的電流C數和時間分別為:2C電流, 5mins。
截止電壓採最低標準判定為10.8V (UPS將停止供載條件)。詳細敘述為2C電流針對電池放電,需要持續5 mins維持電池端電壓在10.8V以上,稱為正常的電池。
另外,參考截止電壓標準設定之依據 圖1,調整電池放電截止電壓為11.2V (IEEE-1188電池容量80%判定)。
圖1、截止電壓標準設定

綜合以上的條件我們使用 圖2來談談原先廠內對於UPS電池管理的條件:將全部的電池分為三類,分別是A類、B類以及C類。
圖2、電池管理的條件

A類電池:放電截止電壓>11.2V,我們稱為健康電池無需更換。
B類電池:放電截止電壓介於10.8~11.2V之間稱為堪用電池,需要再深入評估電池狀況,是否需要更換或持續運轉。
C類電池:放電截止電壓<10.8V,明顯的放電截止電壓不足,有立即風險需要即刻更換電池以確保UPS系統的穩定性。
A、C類電池有很明確的定義,且為已知的狀況;但反觀B類電池,亦稱為堪用電池,所謂的堪用究竟還可以撐多久?是否需要提前更換?
畢竟以一個晶圓廠區上萬顆的電池,能多運轉一年就是對於節費多一分幫助,但站在考慮到系統的穩定性面來看,我們更希望能盡速汰換掉這些有疑慮的電池。若是能夠有個手法可以讓我們預知這些B類電池究竟還能夠運轉多久?是否需要當年度即刻汰換?就是本文所探討的方向。
本文所提出的手法,時間點在進行2017年度電池放電保養前夕,經歷了保養紀錄系統建置,為了保養明確化以及資料減量,我們釐清那些大量且冗長的保養過程紀錄值,並思考是否不再留存這些資料紀錄,順帶思考了過去近十年所留存紀錄的資料到底有什麼用途?
畢竟現在看到的狀況是所謂的良好標準,以當時的解讀是一個不會有危險的標準,所遵照的經驗法則常常是無法具體描述真因的一個現象,目前流行的一個口號叫做大數據分析,想想大數據是有了但是要怎樣分析呢?
關於電池的保養測試,我們能夠有哪些資料?電池電壓、溫度、使用年份、廠牌型式、使用負載率。在這樣無所適從的狀況之下,認知上電池從有電到沒電最明顯的就是電壓變化,那麼對於很有電的電池來說是不是就是它變化會較少,況且現行使用上電池的分壓不均現象也時有見到。
循這樣萌芽的念頭,嘗試將這些電池保養紀錄的資料轉換,透過實驗驗證後,並經過這個參數創造及一連串的資料整理,將2017年判定為異常的電池結合2016年的電池資料透過散佈圖進行比對,發現之間存在著高相關的關聯性,於是有了∆V (Delta Voltage,電壓差)關鍵參數的這個結果。
文獻探討
電池之組成與原理
既然我們將電池分為健康、堪用、以及異常這三類就必須瞭解是甚麼原因造成上述的狀況,透過文獻[1][2][3]皆有提到電池劣化的原因,電池是利用物質的氧化和還原所產生的電能或化學能的原理而誕生的,是目前日常生活與工業應用上最被廣泛使用儲存電能的設備,因此必須具備可攜帶、耐震、耐衝擊、壽命長以及高能量密度等特性,而構成電池的四個主要部分為電極(陽極板與陰極板)、電解液、隔離板、與外部的電槽。
透過電池電極上活性物質與電解液產生化學反應而放出電子,藉由這樣的氧化反應可以從電池得到電能,我們稱之為電池放電;而透過電池外加電能充電,可將化學反應後的物質還原,儲存在電池槽內提供轉換電能之需求。理論的氧化還原反應,能夠百分百的作用,然而實際上的狀況,卻是電解液有一定的壽命,隨著存放的時間拉長或是氧化還原反應的頻繁,部分電解液分子會形成惰性結晶附著於電極板上,將無法有效的與電極產生化學反應放出電子,就是我們所看到電池放電電壓未達合格標準的紅燈狀況。
電池健康狀態與定義
從電池的組成原理了解到電池劣化的原因,但我們實務上使用卻無法拆卸電池槽來觀測內部結晶狀況來得知電池的健康狀態。實務上的電池健康狀態評估參考文獻[10]動態電池健康狀態檢測手法常見的有開路電壓法、加載電壓法、內阻偵測法,以及庫倫估測法。目前廠內用來判斷電池健康狀況的手法為加載電壓法以及內阻偵測法。
加載電壓法
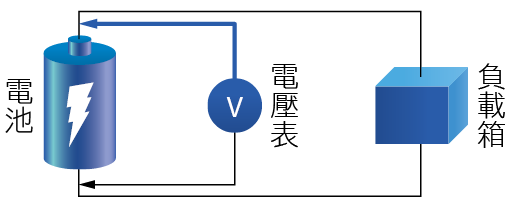
電池接上負載在使用狀態下如 圖3,利用電池在放電截止電壓前,電池端電壓隨著放電時間線性減少的關係來預估電池的殘存電量。於量測時紀錄輸出端電壓,透過截止電壓來判斷電池的健康狀況。
圖3、加載電壓法量測圖
內阻偵測法
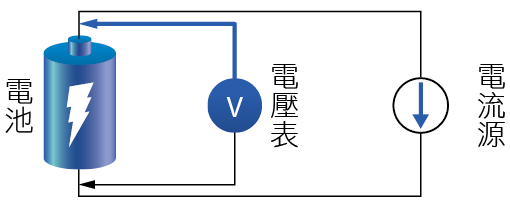
透過量測電池充放過程中的內阻變化 圖4,對照內阻與電池容量的關係來評估電池容量。一開始先量測電池的開路電壓,接著在迫使電池瞬間輸出一定電流而使電壓隨之降至一定值,此時內電阻值即可由式(1)得到。

其中,
Rin:電池內阻值
Voc:電池開路電壓
Vdis:電池放電時電壓
I:測試放電電流
廠內透過上述兩項手法來評估電池是否達到更換條件。
圖4、內阻偵測法量測圖
理想電池與實際電池的差異
文獻[4]陳敏睿、賴彥廷,不斷電系統鉛酸電池活化再生應用分析提出電池是一種用來儲存化學能,將化學能轉成電能的應用裝置,是一種可攜式的能量。理想的電池輸出電壓為定值,不會受到任何因素影響。但事實上,實際電池輸出、入特性會受到許多因素的影響而改變。因此實際電池在作功時,電池的端電壓會下降。本文所提到的鉛酸電池,正極為多孔性的二氧化鉛,負極為海綿狀的鉛,極板上面的活性物質與電解液中的硫酸產生化學變化而放出電子,每一單位(Cell)至少可提供2.04伏特(V)的電壓,下面列出電化學反應式:
放電反應式正極:
PbO2 + 4H+ + SO42−+ 2e− →2H2O + PbSO4
放電反應式負極:
Pb + SO42− → PbSO4 + 2e−
放電總反應式:
PbO2 + Pb + 2H2SO → 2PbSO4 + 2H2O
充電反應式正極:
PbSO4 + 2H2O→ PbO2+ 4H+ + SO42−+ 2e−
充電反應式負極:
PbSO4+ 2e− → Pb + SO42−
放電總反應式:
2PbSO4 + 2H2O→ PbO2+ Pb + 2H2SO4
文獻[5][6]湯淺電池與CSB電池提到當放電時電解液的四氧化硫進入正極板上,與正極板上的二氧化硫結合,此時正極板會釋放出氧氣進入電解液中,所以電解液的含水量會增加,也就是電解液的比重會降低。電解液中的四氧化硫會進入負極板中與鉛結合成硫化鉛,如此電解液中的四氧化硫減少,電解液的比重又降低,所以電池中的電力降低。
數次的循環充放電後,會有部分的化學物質無法完全透過充電還原,導致電池健康狀況的衰減,也代表著完全反應化學變化的時間隨之減短,電解液的比重降低更為快速,因此我們透過放電所量測的電池端電壓,相較於新品健康電池也掉得更為嚴重。
電池的內部電壓和電解液濃度成比例,電池在放電時的電壓變化,因放電電流和電池的內部電阻之間有關係。
E (端電壓) = E0 (內部電壓) − I (放電電流)× r (電池內部電阻)
從此式得知放電電流愈大電壓的下降也愈大,代表著電池端電壓(E)會隨著電池所剩餘的容量減少而下降。
數據分析模式
透過放電行為前後所得到的電池端電壓,就是本文提到的電壓差。因此,電壓差代表著這顆電池的健康狀況。我們可得知的是相對電壓差小的電池,健康狀況比電壓差大的電池來得優良。如此一來我們僅得知相對的現象,仍然無法切確的找出異常的電池甚至無法使用回顧文獻所提供的模型,因為,並非同樣的充放電參數都適用所有的電池。
本文使用歷年電池紀錄的數據,建立一個適合的模型,用以推估電池的健康狀況,以達到電池異常即早判斷的手法。
大數據的概念
文獻[14]陳欣得在2006年敘述統計學提出大數據的幾個精神就是:不用取樣。樣本=母體、不在乎因果關係,在乎關聯性、把一切資訊給資料化。巨量的定義,不在於多寡,而在於「完整」。然而大數據的範圍涵蓋甚廣,定義也多有分岐。2001年Gartner公司的分析師Doug Laney首先在其發表的文章中強調資料處理的三個關鍵:資料量、速度以及多樣性,並在2012年重新定義大數據:「大數據是大量、高速或類型多變的資訊資產,他需要全新的處理方式去促成更強的決策能力、洞察力與最佳化處理。」
散布圖
根據文獻[15]江明諺在大數據下的糖尿病醫療管理提出在統計分析生物或是醫療資料時,當我們要探討兩個連續型變量(continuous variables)的關係時,比如說父母身高跟小孩身高的關係、一個人身高跟體重的關係等等,最好的方法便是先作圖(visualization),此時散布圖(scatter)便是很好的工具。而我們把資料用散布圖呈現的時候,另一個重點便是要去思考這兩個變量的關係。
但兩個變數之間會有什麼關係呢?往往都是以「不確定的函數關係」存在。這時候常常會先尋找,這變量間是否可以用相關(correlation)或是回歸(regression)分析去解釋變數之間的聯繫。
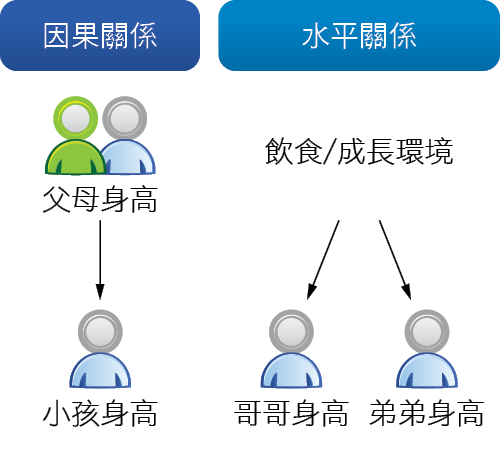
連續變數間最常見的關係便是:因果關係、平行關係 圖5。因果關係是指一個變量受另一個變量影響,而平行關係通常代表兩個變量同時受某個因素影響。譬如小孩身高受著父母身高的影響為因果,兄弟的身高變異受著飲食、環境等的影響稱為水平關係。
圖5、散布圖因果關係和水平關係
觀察變量間的關係性質、類型與程度就可以決定用相關分析或是回歸分析來探討兩個變數,當使用回歸分析的時候,通常就是假定一個變數主要受另一個變數影響,被影響的變數通常稱為應變量(dependent variable),常用y表示,影響別人的變數通常稱作自變量(independent variable),常用x表示。
當兩個變量間為平行關係時,可使用相關分析,此時兩個變量間其實沒有應變量和自變量的差別,且兩者同時都存在隨機誤差。對兩個變量間的直線關係進行分析則稱為直線相關分析(linear correlation analysis)或是簡單相關分析(simple correlation analysis);而兩個變量間為因果關係時,我們使用回歸分析,此時應變量(dependent variable)隨自變量(independent variable)改變,且應變量伴隨者隨機誤差存在,當研究一個應變量與一個自變量的關係則稱為一元回歸分析(one factor regression ana-lysis),研究多因一果實,則稱為多元回歸分析(multiple regression analysis)。
研究方法
套用上述大數據的管理概念,所謂的大數據並不著重於取樣的技術,而是直接使用數據的母體來取得我們要的答案,用來預知B類電池在異常前會有甚麼樣的徵兆。我們可以利用過去放電保養所記錄的龐大數字來找出異常電池共同點,找出異常電池的特徵。
大數據普遍應用都是使用散布圖來分析個變數的關係性質,找出變數之間的因果關係又或是水平關係,本文使用的是水平關係 圖6。
圖6、數據管理以及分析流程
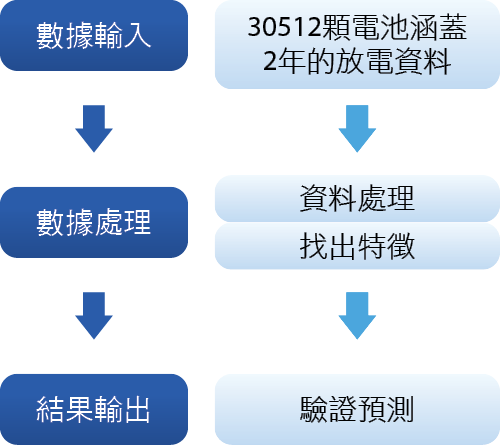
本次實驗輸入了廠內所有電池紀錄於2016年以及2017年的放電保養資料,透過第一次散布圖分析後移除離群的資料,並將2016年處理後的資料製作了第二次的散布圖,透過2016年資料作成的散布圖比對2017年資料找出異常電池的模型。最後根據我們所要求的準確度選擇Cut-Off line來決定我們的∆V,應用∆V和截止電壓來推估2018年的電池狀況,並完成是否即早PM更換B類電池的目的。如此一來,可以達到電池異常預知判斷的目的。
數據輸入
我們要驗證2017年電池的∆V,因此必須取得2017年以及2016年電池的保養所有資料。將廠內30512顆電池兩年資料建檔,共計61024筆資料。每筆電池資料包含放電前電壓、放電後電壓以及異常標記 表1。
|
電池編號 |
2016年 |
2017年 |
||
|---|---|---|---|---|
|
放電前電壓 |
放電後電壓 |
∆V |
放電異常電池 |
|
|
電池1 |
12.1 |
11.8 |
0.3 |
|
|
電池2 |
12.2 |
11.8 |
0.4 |
V |
|
… |
… |
… |
… |
… |
|
電池30511 |
12.1 |
11.9 |
0.2 |
|
|
電池30512 |
12.1 |
11.9 |
0.2 |
|
資料處理
篩選出2017年異常的電池將其標記。接著,彙整標記電池2016年的放電前後電壓,並計算∆V。將這30512筆電池的資料製作成散布圖,並篩掉離群的數值後可以得到我們所需要的散布圖。最後在這個散布圖上可以看到每顆電池的放電後截止電壓和∆V 圖7。
圖7、2017年檢測異常電池在2016年放電資料散布圖1
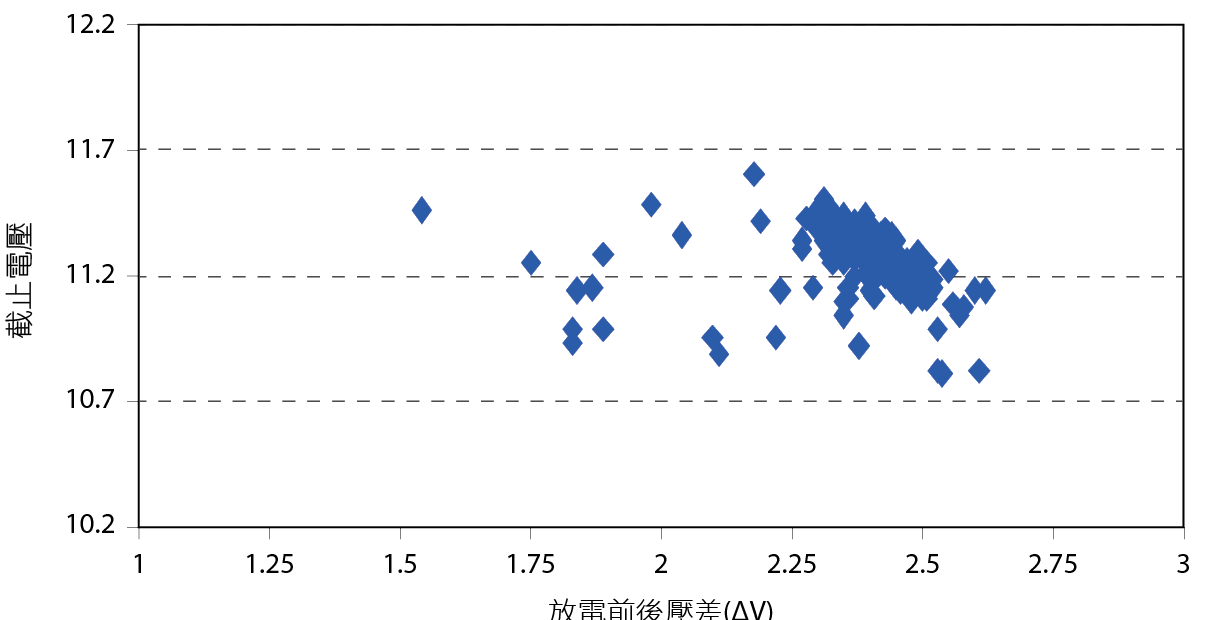
找出特徵
觀察 圖7,可以發現這些異常的電池分布似乎有集中在某幾個區塊的趨勢。於是我們A、B、C類電池的標準標上紅線使其散布圖變成 圖8。
圖8、2017年檢測異常電池在2016年放電資料散布圖2
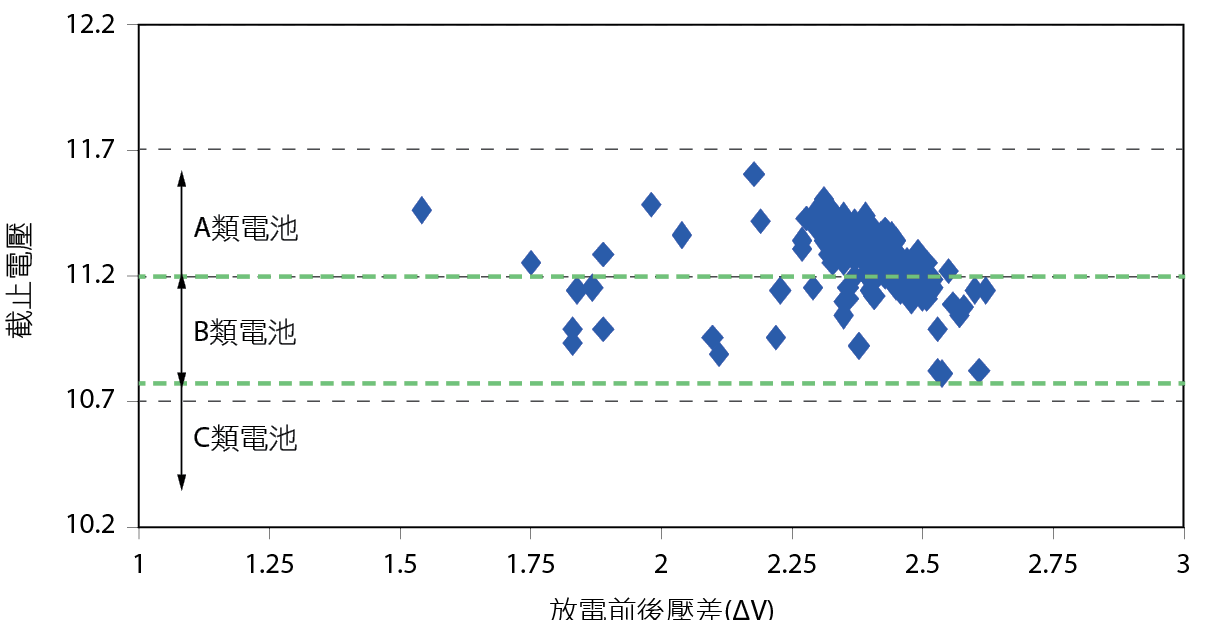
透過 圖8可以明顯看出來原本在2016年判斷為A類電池,卻在2017年變成異常需更換的電池,這驗證了本文的推論:電池異常即早PM判斷手法除了截止電壓之外,還存在著一個共同的特徵─就是∆V。
接著我們必須把∆V的分界線畫出來,並移除C類電池的判斷線(因為C類電池為當年度立即更換,因此並沒有預測電池即早PM的需求),我們先設定一個∆V=2.3V的分界線畫上即成了 圖9,透過四個象限的標示可以更明顯的區分出2017年度檢測出異常的電池,它在2016年的保養資料是落於第I、III、IV象限且佔總數的93%。
驗證預測
為了驗證是否正常的電池會散布在第II象限,我們撈出2017檢測正常的電池2016年資料,並加入在 圖9內。
圖9、2017年檢測異常電池在2016年放電資料散布圖3
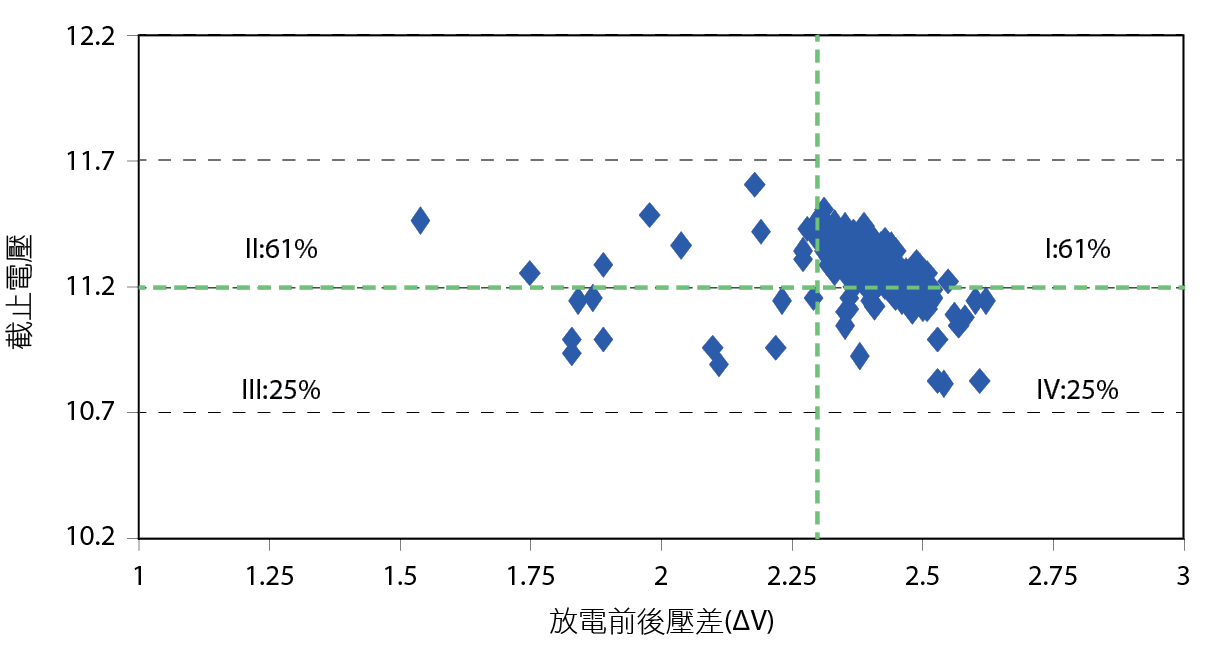
如 圖10所示,異常品在2016年的分布確實集中於第I、III、IV象限,而健康電池在2016年是集中於的II象限。由此可推斷只要透過正確∆V分界線的選擇,我們可以有效預測明年度異常的電池。儘管會誤殺到明年度檢測仍為正常的電池,但佔比遠小於5%。
圖10、2017年檢測異常電池在2016年放電資料散布圖4
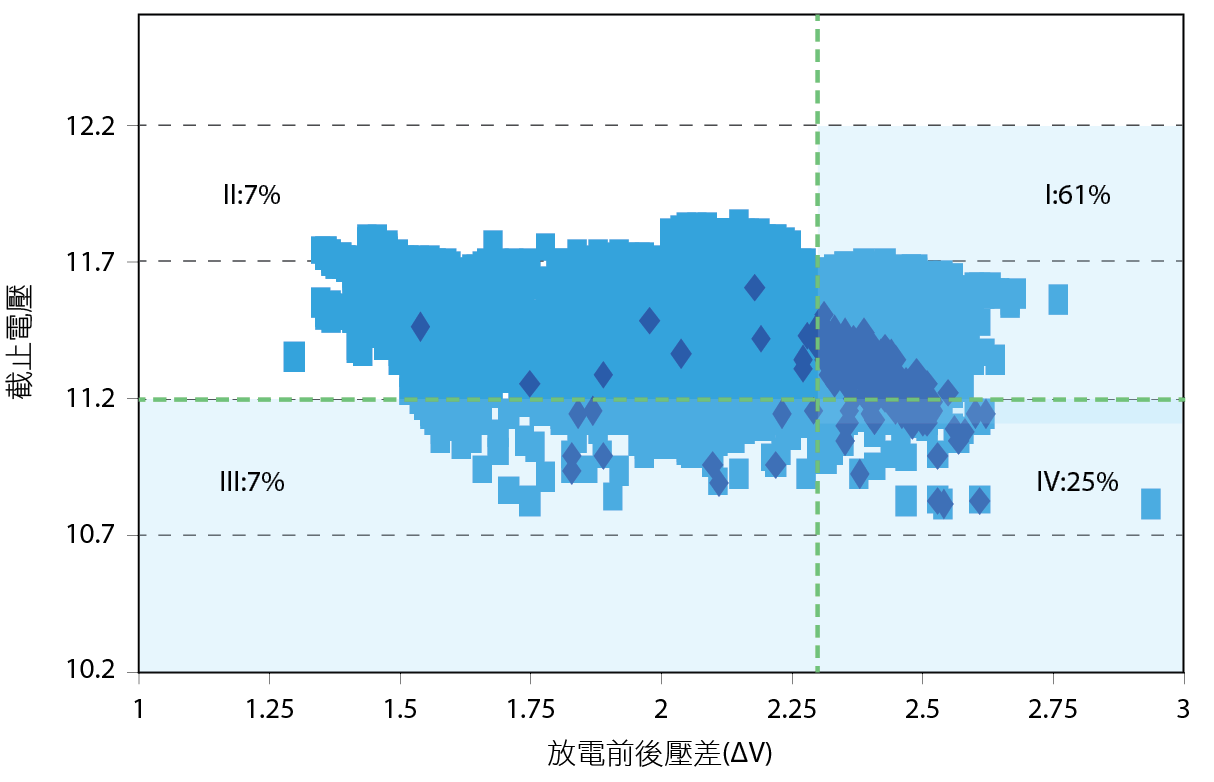
結果與分析
∆V分析與選用
在電池放電的大數據中,我們選定了Y軸(截止電壓)的設定門檻,接下來我們必須探討X軸(∆V)的門檻設定。標記2017的異常品,套用在2016年的散布圖上。觀察2016年∆V=2.25v時 圖11,可以有效地預測並抓取到95% 2017年的異常電池;∆V=2.3v時 圖12,則撈取的異常電池比例為93%。
圖11、ΔV=2.25v選用的散布圖
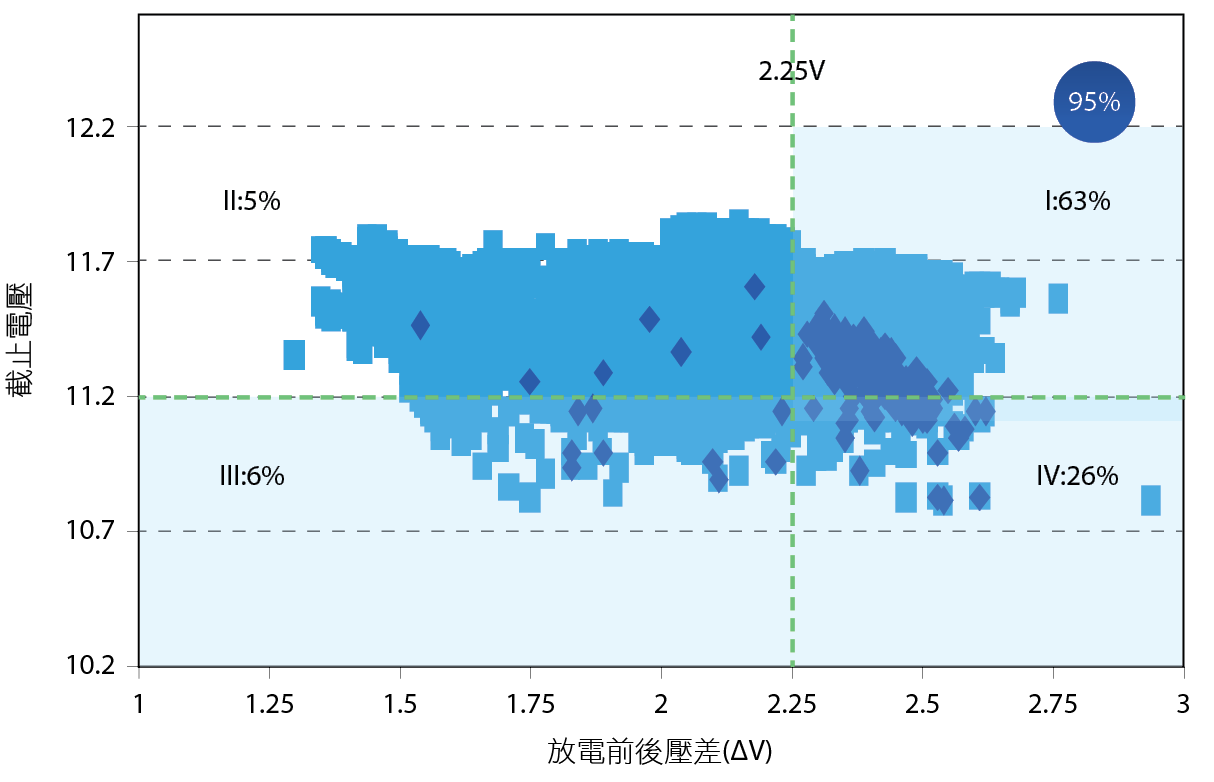
圖12、ΔV=2.3v選用的散布圖
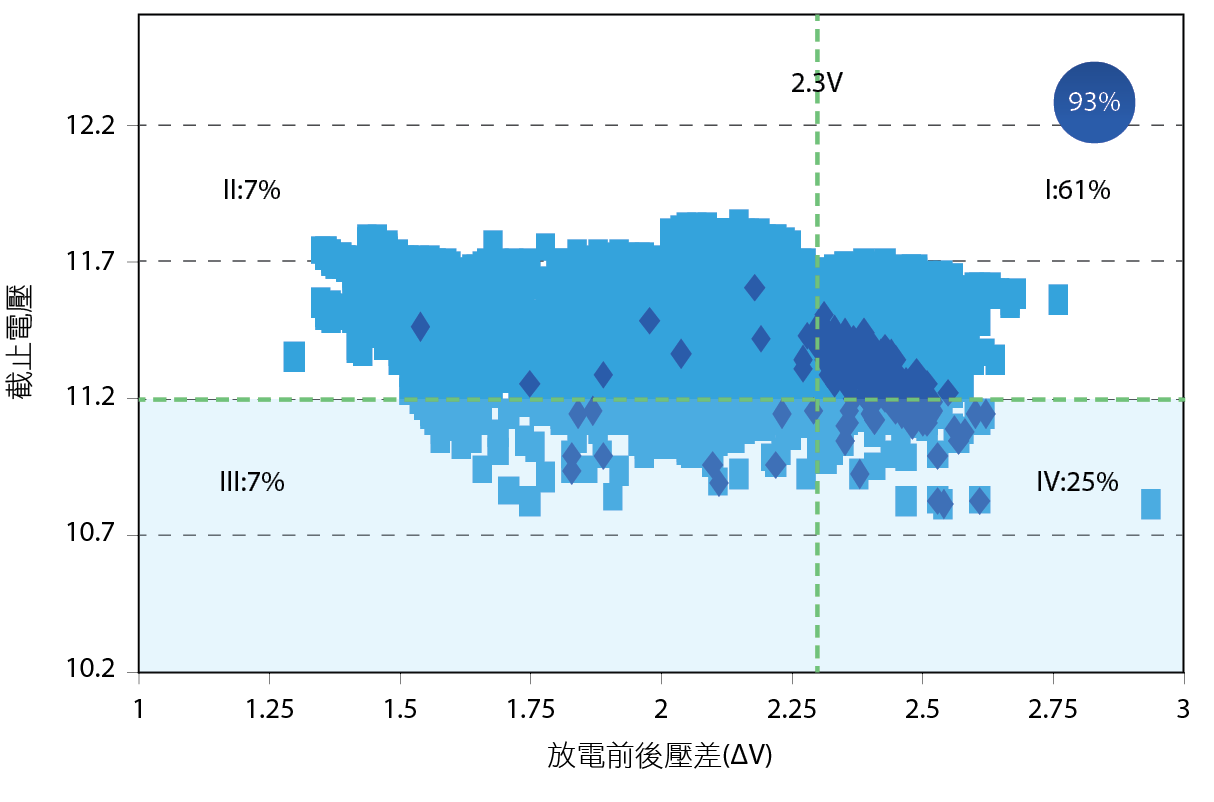
舉例來說,套用∆V=2.3v的分析,我們可以在2016年時規劃更換這些被預測即將異常的電池,則2017年的異常電池率將可大幅降低為原本的7%。
如此一來,∆V電壓的選用將變得更為彈性,各使用者可根據更換成本和UPS系統可靠度這兩者取得平衡點或根據各廠區描定的異常率來決定,為各自廠區找出最適合的模型。以竹科A廠為例:
- 2.25V:異常電池涵蓋率95%,需更換電池約1500EA
- 2.3V:異常電池涵蓋率93%,需更換電池約1000EA
本文選用∆V=2.25v為Cut-off線做為標準,目的在於撈出95%的異常電池,並將電池異常率控管在0.1%以內。
∆V的應用
異常電池率降低(防範未然),使用∆V手法提早篩選容量衰減較大的電池。依資料模擬若2016年執行,在2017年的異常電池數量將減少為15顆,異常率估計下降為0.05% 表2。
|
項目 |
電池狀態 |
||||||||
|---|---|---|---|---|---|---|---|---|---|
|
在線時間(年) |
0~1 |
1~2 |
2~3 |
3~4 |
4~5 |
5~6 |
6~7 |
7~8 |
Total |
|
電池顆數 |
240 |
887 |
6,254 |
6,577 |
5,274 |
1,840 |
9,360 |
80 |
30512 |
|
電池占比 |
1% |
4% |
20% |
23% |
10% |
2% |
40% |
0% |
100% |
|
Spec.10.8V |
- |
4 |
27 |
20 |
8 |
4 |
230 |
- |
293 x 5% = 15顆 |
|
Spec.10.8V |
4 |
7 |
11 |
11 |
10 |
105 |
3 |
151 |
|
|
Spec.10.8V |
0.0% |
0.5% |
0.4% |
0.3% |
0.2% |
0.2% |
2.5% |
0.0% |
1.0% → 0.05% |
|
Spec.10.8V |
1.7% |
0.8% |
0.2% |
0.2% |
0.2% |
5.7% |
0.0% |
0.0% |
0.5% |
∆V的實際使用
透過2016以及2017年的電池資料找出了電池即早PM判斷手法,接下來我們將這樣的手法正式套用到2018年(即為2017年先預測明年度可能異常的電池,並完成新品更換)。
以竹科A廠為例, 表3所示2016年異常率為0.5%;2017年異常率為1.0%,異常率逐年倍增是由於廠內的十年期電池有四成以上皆運轉了7年,電池大批次逐漸老化,我們由此推斷若不使用∆V手法即早更換PM,至2018年異常率將會達到2.0%。但透過本文提出的手法,有效的將異常率控管在1.0%以下。
|
項目 |
電池狀態 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
在線時間(年) |
0~1 |
1~2 |
2~3 |
3~4 |
4~5 |
5~6 |
6~7 |
7~8 |
8~9 |
Total |
|
2018電池顆數 |
1,306 |
2,601 |
1,349 |
7,107 |
6,546 |
4,480 |
920 |
6,805 |
78 |
31,192 |
|
電池占比 |
4% |
8% |
4% |
23% |
21% |
14% |
3% |
22% |
0% |
100% |
|
2017電池顆數 |
1 |
480 |
1,350 |
7,135 |
6,576 |
4,491 |
1,760 |
8,641 |
78 |
30,512 |
|
電池占比 |
0% |
2% |
4% |
23% |
22% |
15% |
6% |
28% |
0% |
1 |
|
2016電池顆數 |
- |
- |
1,110 |
7,135 |
6,577 |
4,491 |
1,880 |
8,641 |
78 |
29,912 |
|
電池占比 |
0% |
0% |
4% |
24% |
22% |
15% |
6% |
29% |
0% |
1 |
|
Spec.10.8V |
1 |
3 |
3 |
44 |
38 |
20 |
1 |
112 |
- |
222 |
|
Spec.10.8V |
1 |
- |
1 |
32 |
20 |
8 |
4 |
233 |
- |
299 |
|
Spec.10.8V |
- |
- |
4 |
7 |
11 |
11 |
10 |
105 |
3 |
151 |
|
Spec.10.8V |
0.10% |
0.10% |
0.20% |
0.60% |
0.60% |
0.40% |
0.10% |
1.60% |
0.00% |
0.70% ↑ 1.0×2=2.0% |
|
Spec.10.8V |
100% |
0.00% |
0.10% |
0.40% |
0.30% |
0.20% |
0.20% |
2.70% |
0.00% |
1.00% ↑ 0.5×2=1.0% |
|
Spec.10.8V |
0.00% |
0.00% |
0.40% |
0.10% |
0.20% |
0.20% |
0.50% |
1.20% |
3.80% |
0.50% |
結論
透過統計手法加上原廠測試驗證,等於11.2V加∆V(2.3V),確實有效的降低電池異常率,並將其控管在1%以內。最後再將2018年的異常品驗證2017年的分布狀況,觀察 圖13可以發現,第 I、III、IV象限的異常電池已於2017年預知更換,由 圖14觀察得知,原本可能會發生的2%異常率下降至0.7%。
圖13、2018年異常品在2017年放電資料散布圖
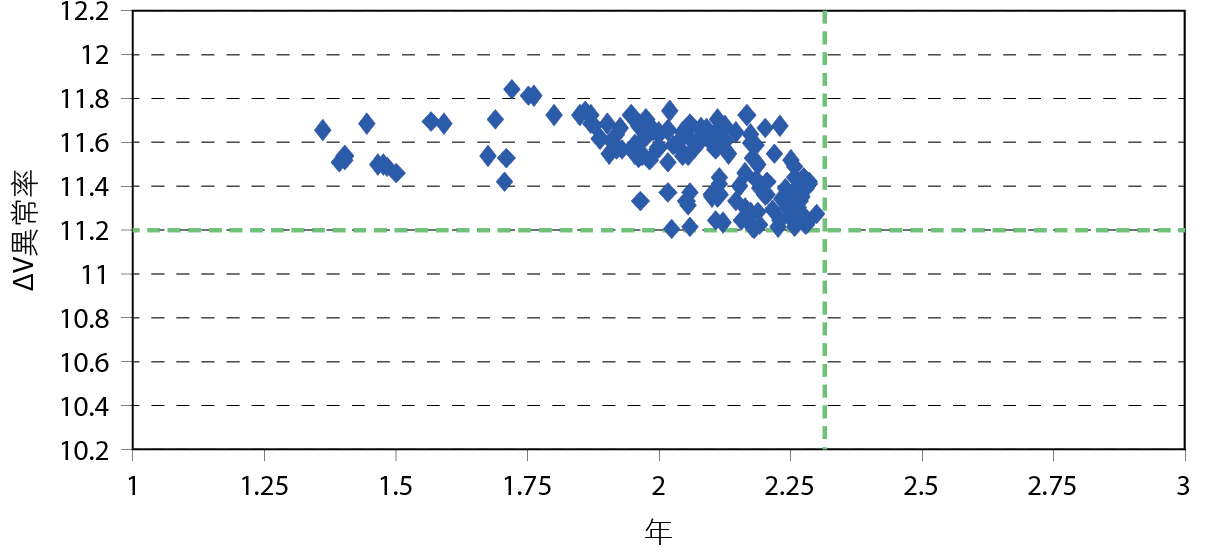
圖14、2018年異常品在2017年放電資料散布圖
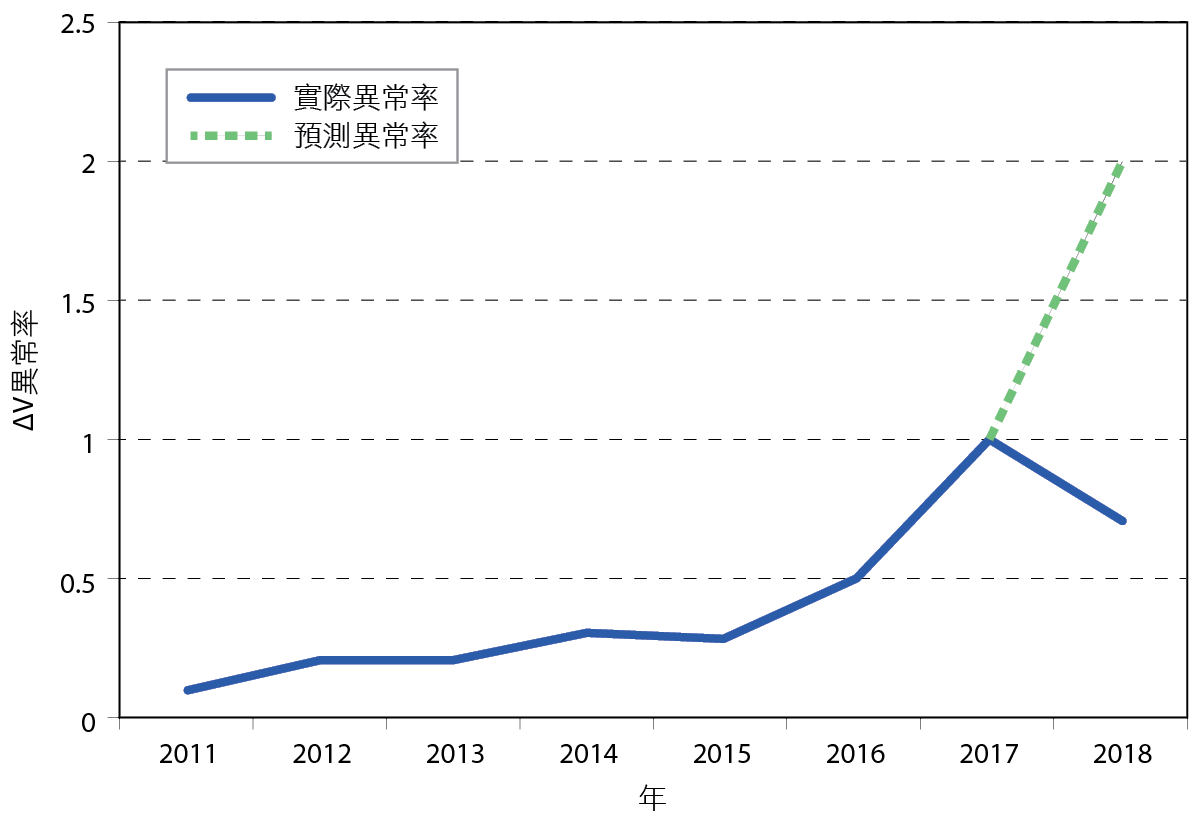
雖然我們使用本文手法大幅改善電池的異常率,但並未如預期的準確。參照 表4,原先我們選擇模型11.2V+∆V(2.3V)預測可以撈到95%的異常電池,理當可以將異常率降低為0.1%,但透過2018年實際驗證僅撈到65%的異常電池,原因在於電壓的取樣。
|
選擇∆V=2.3V(撈取95%資料) |
未使用∆V異常率 |
預估使用∆V異常率 |
實際使用∆V異常率 |
|---|---|---|---|
|
2016 |
0.5% |
- |
- |
|
2017 |
1% |
0.05% |
- |
|
2018 |
2% |
0.1% |
0.7% |
由於∆V是初始電壓與截止電壓的壓差,因此初始電壓與截止電壓的正確性就佔了很大的因素,說明目前UPS電池放電手法並不固定,有兩項差異左右了這個∆V的值,也決定了這個手法的準確性。
- 電池充電狀況:電池在放電保養前,飽電與否會影響初始電壓與截止電壓的量測值。
- 電池放電C數:我們使用電池標稱的AH數來決定放電的C數,但並非所有的電池實際AH數如同標稱,這會造成放電C數不匹配,進而導致誤判放電結果。
∆V是放電前後的電壓差異,使用∆V和截止電壓搭配使用,確實能有效的找出即將異常的電池,也能夠根據歷年的資訊來預估明年的電池衰減狀況,提前規劃維護,實現所謂的「預知保養」。
事實上對於本文的分析需要多次的資料驗證比對,儘管當初預估使用大數據分析能夠將其他的變數忽略掉,但由2018年的檢測結果也顯示事情並不是像想像中簡單,充電狀況以及放電C數大大的影響著我們的預測結果與準確度。
但期望能夠透過這樣篩檢的減量更換後,隔年的電池異常率能夠維持在0.1%的目標,本文手法主要分析更換高年份的電池,在減量更換且降低異常率是有所幫助的,這讓我們對於本文提出的分析手法是有信心,如果我們能夠在將條件訂定更加明確的分類、比對,如檢測統一標準化:不同充電模式的分開、不同年份的分開、電池每年的電壓下降幅度等等區分後資料加以比對分析,或許我們能夠創造出所謂的電池更換公式。那麼電池異常即早PM的判斷手法將可以達到接近100%的預測效果。
參考文獻
- Nattapat Praisuwanna, SurinKhomfoi “A seal lead-acid battery charger for prolonging battery lifetime using superimposed pulse frequency tech-nique” 2013 IEEE Energy Conversion Congress and Exposition.
- LeventeSzabó, Dan Pitica, Ovidiu Pop “The voltage response of lead-acid battery through pulses charging with variable frequency and duty cycle” 2016 39th International Spring Seminar on Electronics Technology (ISSE).
- S. Schilling “Ensuring lead-acid battery performance with pulse technology” Fourteenth Annual Battery Conference on Applications and Advances. Proceedings of the Conference, 1999.
- 陳敏睿,賴彥廷,不斷電系統鉛酸電池活化再生應用分析,2016新竹科學工業園區廠務技術研討會
- 湯淺電池公司網站,http://www.yuasa.com.tw/
- CSB公司網站,http://www.csb-battery.com/
- 碩成電子(股)公司/日商心榮通商(股)公司,電池活化器(AP)測試報告,2017
- 古河電池株式會社,蓄電池の壽命推定方法および蓄電池の壽命推定裝置,https://astamuse.com/ja/published/JP/No/2007271438
- 台灣積體電路製造股份有限公司,F- CEC-02-03-008 300MM FAC UPS P.M. O.I.
- 黃柏漢,翁國樑,林登禾,林明志,動態電池健康狀態檢測手法,第十三屆電力電子研討會
- T. Yanagihara and A. Kawamura, “Residual capacityestimation of sealed lead-acid batteries for electric vehicles,”Power Conversion Con-ference, pp. 943-946, 1997
- 電動車充電對電力品質及電力供應影響之研究,台灣電力股份有限公司
- 賴世榮,智慧型鋰離子電池殘存電量估測之研究,國立中山大學電機工程學系碩士論文
- 陳欣得,敘述統計學,2006
- 江明諺,大數據下的糖尿病醫療管理,國立中山大學企業管理學系碩士論文
- 淺思考:散布圖(scatter chart)、相關(correlation)和回歸(regression),https://weitinglin.com

留言(0)