摘要
本文提供一套全新的AMC管理方式,透過AMC濃度分布圖視覺化效果,提供廠區完整且直觀的污染區,掌控該區AMC濃度分布狀況,當FAB發生AMC異常時,可加速改善和有效防止污染區擴大。
前言
隨著半導體製程的快速演進,製程越來越精細,無塵室生產環境潔淨度也日益嚴苛,而AMC管理控制更是影響良率的關鍵因數之一。許多文獻研究指出AMC對製程的重要影響,如造成晶片腐蝕、線寬的改變、膜厚降低及電性的改變等影響製程良率問題。因此,廠區針對AMC污染物監測,每年投入大量的分析儀器設備成本及人力巡檢資源 ,面對更為嚴峻的製程低濃度規格,如何在異常污染發生前快速預警及降低人員查漏時間等問題上,以更有效的AMC監控方式進行管理,儼然成為現今一大課題。
文獻探討
為了能更有效的AMC管理方式,需發展出一套可總覽無塵室全區的污染物濃度分布圖,提高管理決策的執行,加速污染源的環境改善。但利用有限的已知環境資料點,推估環境未知點位的資料數值,確實是一大新的挑戰。在過去文獻上繪製污染物濃度分布圖的主要方式有兩種 [1],其一為空間推估法(Spatial Interpolation),它是利用空間中已知點的數值,推出空間中其他地方的數值 [2]。其推估法理論所使用參數,僅由污染物濃度及其位置距離所組成 ,並未對其它條件有所限制,優點為參數設定單純,並不需要大量的模擬運算,可以即時出圖顯示。
另一種為計算流體力學(Computation Fluid Dynam-ics, CFD),為一套整合流體力學、數值方法等方式,透過電腦模擬空間中速度場、污染物濃度場等狀況,可更真實呈現實際濃度分布狀態 [3]。但因CFD軟體中需考量較多限制條件,欲執行模擬工作,需提供空間大小,污染源數量 ,及相關機台硬體配置圖以建立基礎模型;亦需調查環境相關設備數據如無塵室空調系統入出口風速、風量、污染濃度讀值、各實體空間(如 : 人數流量、機台設備位置、桌 、椅等障礙物),及污染源位置。其模擬相關資訊皆會影響到模擬結果,且需花費大量時間在模擬出圖,一旦參數設定錯誤,其模擬結果將與實際值相差甚遠。
綜觀上述兩者方法的優缺點,如 表1所示,為因應無塵室即時的參數變化及快速出圖呈現所需,計算流體力學需耗費更多時間在參數的確認及繪圖的製作上,故本文採用空間推估法進行濃度分布圖繪製。常用的空間推估法包括反距離權重法(Inverse Distance Weighted)、克利金法(Kringing)及平滑曲面法(Spline)等,通常資料具備連續性及可傳播的性質時,較適合使用此方法製圖,其中又以反距離權重法及克利金法相關研究居多,例如PM2.5空污地圖 [4]、水源污染的分布 [5]、降雨量分布 [6]等研究。
| 項目 | 空間量測技術 | 流體力學技術(CFD) |
|---|---|---|
| 所需參數 | 污染物的濃度及位置 | 出風/迴風口風速、風量、污染濃度、實體空間障礙物位置、 污染源位置 |
| 優點 |
1.參數單純,可即時出圖 2.不須人為經驗判斷 |
1.考量參數較多,與實際情況較貼近。 2.可模擬預測改善後狀態 |
| 缺點 |
1.需達足夠實際點數目,才能達較佳的解析度 2.無法模擬預測改善後狀態 |
1.若模擬參數假設錯誤,則與實際值差異甚大,需足夠經驗判斷出圖結果 2.出圖計算時間較久,非即時 |
2.1.反距離權重法 (Inverse Distance Weighted, IDW)
針對每一個未知的數值進行推估,反距離權重法是利用鄰近已知點的數值來進行加權運算,所給的權重依照距離遠近來計算,其概念為一個未知的點,它被周圍已知點的值的影響程度與距離成反比 [7],距離越遠影響程度越小 ,影響的程度是以未知點和已知點之間距離的次方表示。公式如下 :
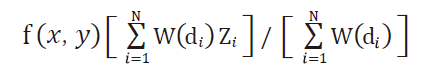
其中W(di)是權重方程式,Zi是第i個已知點的數值,di是i點到未知點之間的距離。
反距離權重法(Inverse Distance Weighted, IDW)之空間內插數學函數,依模式不同搜尋半徑型式(Search Radiu -s Type),可分為可變式(Variable)反距離權重法及固定式(Fixed)反距離權重法。
2.2.克利金法 (Kriging)
克利金法是地理統計(Geostatistics)上的一種方法 [8],在形式上與反距離權重法相當類似,唯獨在權重的運算過程相當複雜,推估未知點的過程第一是空間結構的分析,由已知點的數值來分析資料數值間大小差異和其空間分佈的關係,並產生一個變異圖(variogram)作為內插法適用性的判斷;第二是以平均法或移動視窗法來計算每個網格的數值,樣本點的權重在第一個過程中所產生的空間連續方程來決定。克利金法假設說屬性的空間變異不是完全的隨機性(stochastic)或是完全的決定性(deterministic),而空間的變異包含三要素 : ①空間相關要素;②偏移值(dift)或結構(structure);③隨機誤差。其中偏移值(dift)的存在與否與區域變數的解釋導致了不同克利金法的發展。克利金法在實際運算上分為一般克利金法(Ordinary Kriging,O.K.)與通用克利金法(Universal Kriging, U.K.)。前者假設資料在空間變數不受任何結構因素影響;後者則是假設資料在空間變數上會受結構因素所影響。
一般克利金法(Ordinary Kriging) :
一般克利金法假設偏移值(dift)是不存在的,著重在空間相關要素,衡量所選已知點之空間相關程度的度量是半變異數(semi-variance),公式如下 :
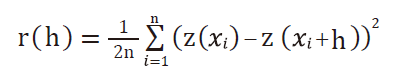
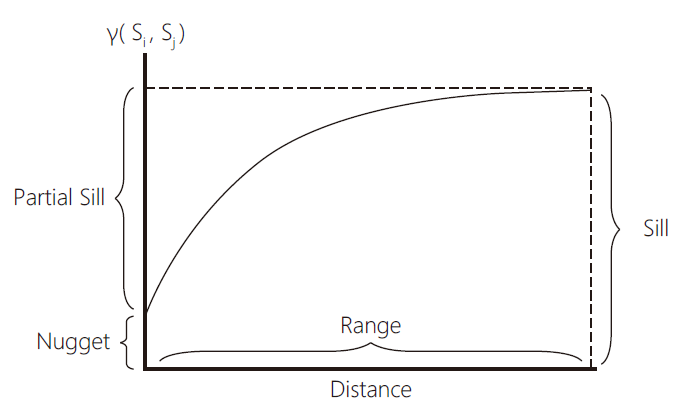
h是樣本點間的距離,n是被h分出的成對樣本數,z值是屬性值。如果在點與點之間有存在著空間相依性,距離較近的點,它們的值會比距離較遠的點的值接近。在具有空間相關性時r(h)會隨著h的增加而增加。在不同距離的半變異數算出後,可繪製出半變異元模型圖(semi-variogram ),y軸代表r(h),x軸代表h,半變異元模型圖,如 圖1所示 ,可分成三部分 : ①碎塊效應(nugget),是在距離為0時的半變異數,代表空間雜訊;②範圍(range),是空間先關部分,它顯示半變異數隨著距離增加,超過範圍的半變異數 ,將是持平狀態;③基值(still),達到持平狀態的r(h)值。
圖1、original半變異元模型圖
半變異元圖將半變異元圖將半變異數與距離聯合起來 ,它可單獨用來度量空間的相關性。但在克利金法中是用來做為內插器,半變異元圖必須與數學函數或模擬(fit),如高斯(gaussian)、線性(liner)、球面(spherical)、圓形(circular)和指數(exponential)模型,各式半變異元模型圖,如 圖2所示。
圖2、各式半變異元模型

擬合(fit)過後的半變異元圖,變可用估算任何給定距離的半變異數。一般克利金法在空間內插中直接使用擬合過後的半變異元圖去估算某點的Z值,公式如下 :
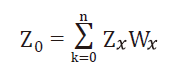
Z0是估計值, Zx為已知點的值, Wx為與每個已知點的關係權重,n是用來估的已知點數量。權重可以從一組聯立方程式求解得到。
通用克利金法(Universal Kriging) :
通用克利金法假設除了已知點之間的空間相關要素外,在Z值的空間變異上是具有偏移(dift)或一個趨勢存在的。一般來說,通用克利金法過程中包含了一階與二階方程式,一階方程式及二階方程式如下。
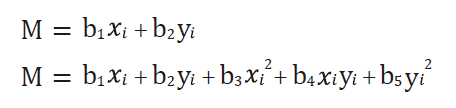
M為偏移, xi和 yi分別為已知點i的y坐標,和為要估計的偏移係數。
克利金法(Kriging)之空間內插數學函數,於一般克利金法(Ordinary Kriging)半變異數型式(Semivariogram Model),可分為球面函數(Spherical)、圓形函數(Circular)、指數函數(Ecxponential)及高斯函數(Gaussian);於通用克利金法(Univer -sal Kriging)半變異數型式(Semivariogram Model),可分為線性函數(Linear with Linear drift)及二次方函數(Liner with Quadratic drift),如 表2所示。
| 一般克利金法(Ordinary Kriging) - 半變異數型式(Semivariogram Model) | 通用克利金法 (Universal Kriging)- 半變異數型式(Semivariogram Model) | ||||
|---|---|---|---|---|---|
| 球面函數(Spherical) | 圓形函數(Circular) | 指數函數(Exponential) | 高斯函數(Gaussian) | 線性函數 (Linear with Linear drift) | 二次方函數 (Liner with Quadratic drift) |
2.3.平滑曲面法(Spline):
利用數學方程式產生一條通過一組已知點的平滑曲線,並依據這一條曲線來推估範圍內每一個定點上的屬性數值,在運算過程中採取最小曲率的概念來進行。在平滑曲面法之空間函數,依模式不同搜尋半徑型式(Search Radius Type),可分為規則型(Reularized Type)及張力型(Tension Type)平滑曲面法 [9],其內插法公式如下 :
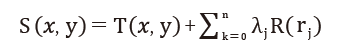
其中,j=1,2…,N (N : 點數), λj : 線性方程式解的係數,rj : 點(x,y)到點 jth的距離。
規則型數學函數 :
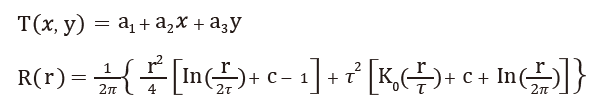
張力型數學函數 :
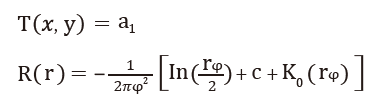
其中,τ2及φ2 : 輸入參數;r : 以知點與未知點間距離;K0 : 模擬數值函數;c : 常數,為0.577215,ai : 線性方程式解的係數。
綜觀上述方法,在反距離權重法與克利金法的比較上,文獻顯示克利金法在估算數值上,呈現較佳的結果。但因權重函數的計算較為複雜,需藉由其他相關軟體(如 : QGIS軟體)使用估算,可作為後續濃度地圖的改良之參考。故本文採用反距離權重法作為濃度分布的估算方式。
計畫方法
本研究主要是藉由無塵室內各區網格的建立,利用現有的已知數據,以反距離權重法進行各區濃度估算,將估算值與實際量測值進行驗證。並將無塵室內各區之污染濃度以顏色分層方式呈現,標示無塵室內污染嚴重之區域。最後,搭配網頁功能輸出,實現AMC視覺化管理模式。
3.1.系統組織架構
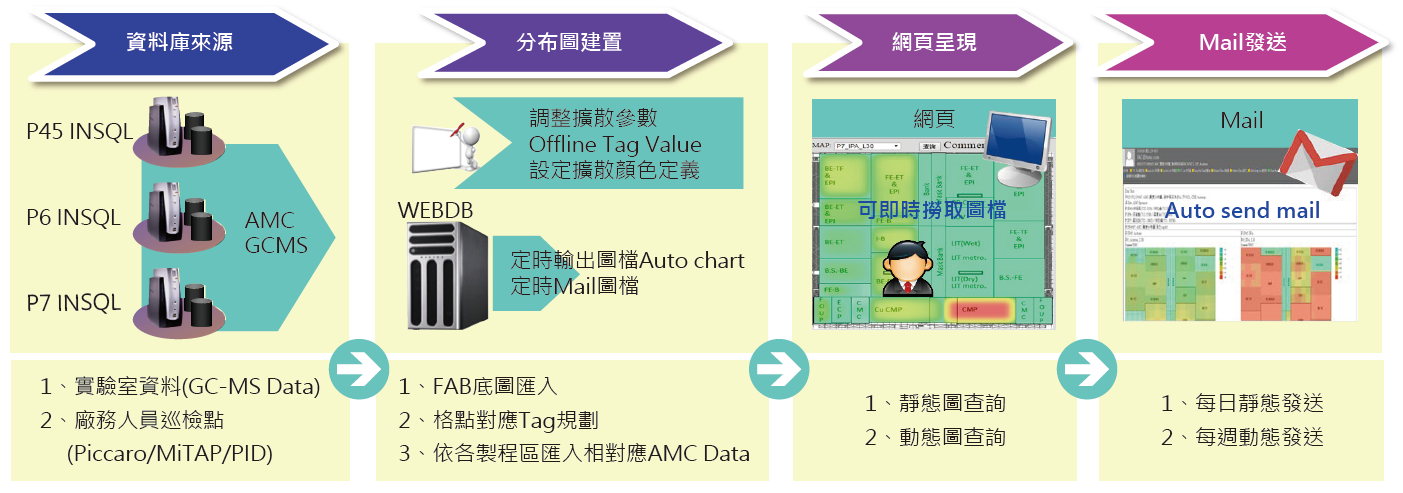
藉由各廠區實驗室儀器(GC-MS)測值及現場人員巡檢資料回傳建立Data Source,再透過TSMC Domain將現場資料存放到各廠SQL Server資料庫,並由網頁即時存取SQL資料庫取得Data,於網頁設定底圖及各格點Tag後,每日與每週分別定時發送靜態及動態Mail,且於網頁可查詢報表。另外於各區域Tag設定OOC/OOS Spec,當廠區觸發OOC/OOS Alert後 ,直接Alert Mail通知給對應窗口,如 圖3所示。
圖3、組織架構流程
3.2.網格模型建置
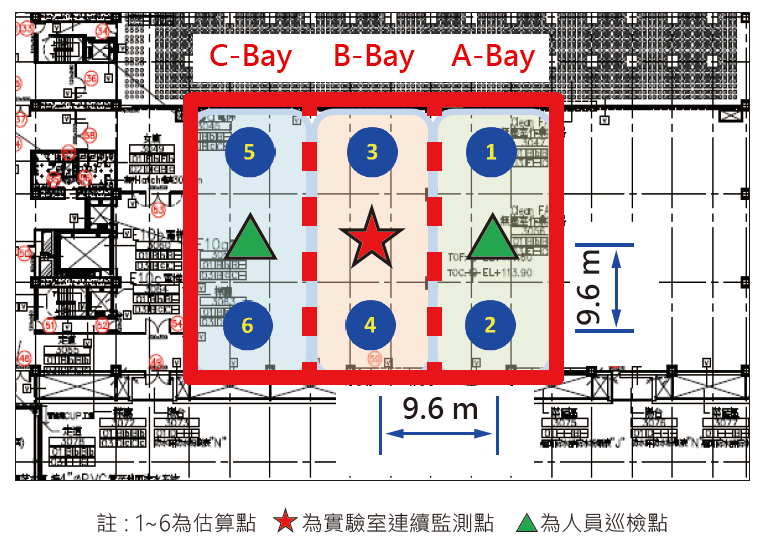
將無塵室各區域進行網格劃分,如 圖4所示,將各區域每條Bay位劃分成三個點位(即該bay前中後三點),格點間採相同距離(約為9.6公尺),並標示實驗室連續監測點及人員巡檢點位置,作為實際資料源的參考位置,利用該點所量測之實際數據,推測其他未進行巡檢之數據,並驗證其推估的準確性。
圖4、網格模型建置
3.3.量測資料收集
在已知量測點的資料建立上,針對無塵室最常監測的四種污染物(TVOC, IPA, Acetone, CXF)進行收集,採用實驗室GC-MS監測點(各區取樣頻率2~3筆Data/天)及搭配人員巡檢點(各區3~4筆Data/天)的量測數據做為已知點位,人員巡檢點針對不同污染物選擇合適的量測儀器,其儀器量測頻率,如 表3所示。但因人員在巡檢點間需要時間移動,故每一區內量測資料並非同一時間的量測數值,而是以該區各量測點間最接近的時間作為最後的資料呈現。
| 儀器種類 | 量測目標物 | 量測週期 | 量測精度 |
|---|---|---|---|
| Online GC-MS | 各種有機物(Ex : TVOC,IPA,Acetone,CXF) | 30min | ppb level |
| Piccaro | CXF | 即時 | ppb level |
| MiTAP | 各種已定義有機物(Ex : TVOC,IPA,Acetone) | 5min | ppb level |
| PID | 總有機物(Ex : TVOC) | 即時 | ppb level |
3.4.濃度地圖建立
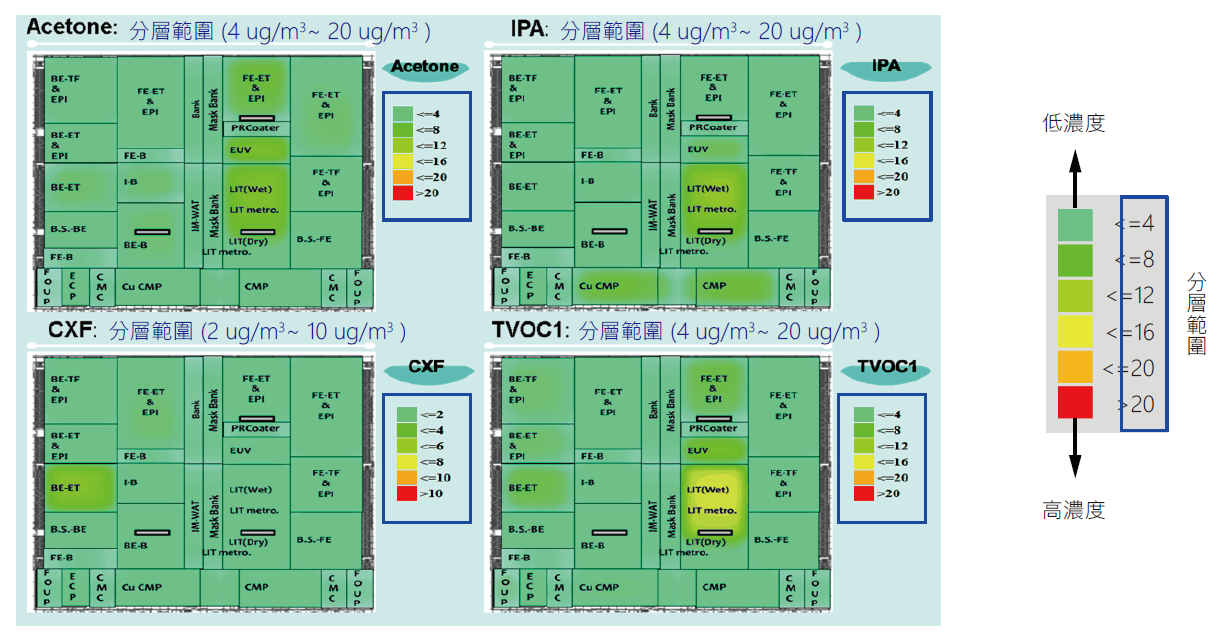
透過實驗室監測點及人員巡檢點的量測數據,應用反距離權重法推估其他估算點數值,即將量測的實際數據與該區對應的網格估算點遠近距離給予相反的權重,以距離的倒數作為權重大小,距離越近權重越大,距離越遠權重越小等方式進行濃度分布圖建置。將無塵室四種污染物(TVOC, IPA, Acetone, CXF)進行繪製,利用相對色階作為濃度分布圖圖層顏色的基準,即由最低至最高濃度採以淺色(藍色、綠色)→黃色→橘色→紅色漸層方式呈現,如 圖5所示,顯示管理決策的優先性,並將不同污染物給予各自所對應的濃度分層範圍。
圖5、濃度分層色階&分層範圍
3.5.網頁功能輸出
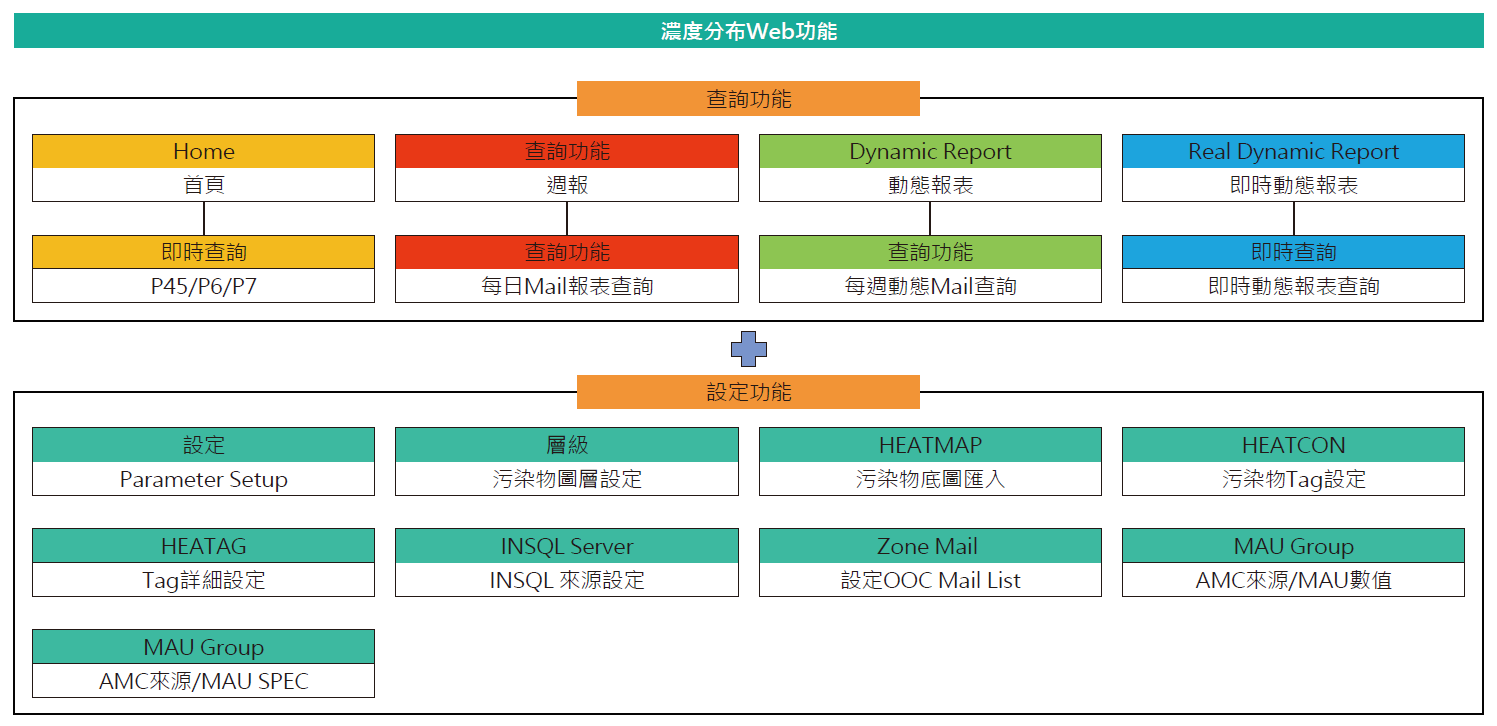
網頁功能主要分為查詢功能及設定功能,查詢功能上包含線上查詢及報表查詢功能,可供人員進行進資料查詢與確認 ;設定功能則可因各自廠區需求,定義相關圖層設定及輸出功能,如 圖6所示。
圖6、濃度分布網頁功能總攬
結果與分析
4.1.濃度分布圖與實際測值比對
將濃度分布圖估算值與實際量測值進行比對,如 圖7所示,可發現兩者平均相差約2~5ug/m3,誤差範圍在10%左右 。其誤差範圍除受到取樣點數量多寡影響外,另一個原因可能來自於空間分析法技術,因所需參數僅考慮室內污染物濃度 ,並無特別考慮其他所有參數,如 : 出風/迴風口風速變化、出風口/迴風口污染物濃度變化、各實體空間條件(如機台位置 、桌、椅等障礙物)。在考量參數較多的情況下,與實際狀況應較為貼近。
圖7、估算值與實際值比對

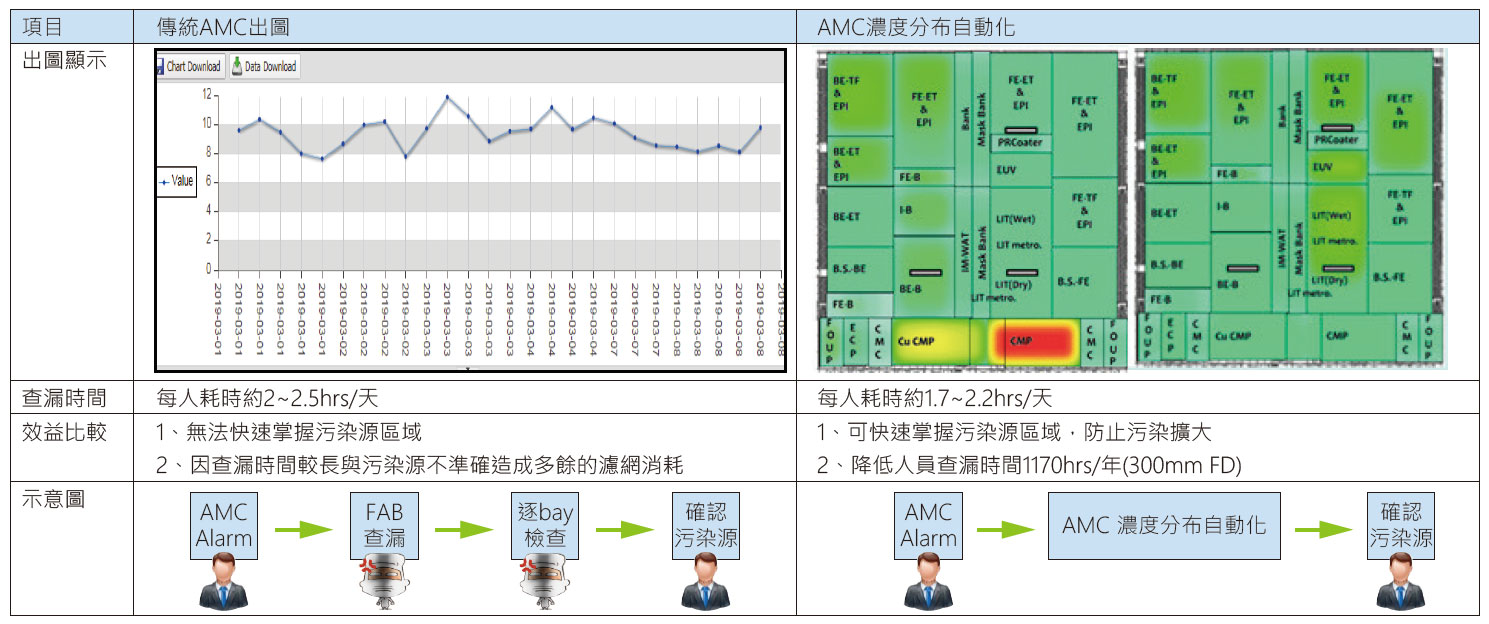
4.2.傳統出圖V.S.濃度分布圖
與傳統AMC出圖方式比較,如 圖8所示,AMC濃度分布圖採用顏色分層的視覺化效果,清楚呈現無塵室內部各區域的AMC濃度狀態,在污染物發生的同時,可快速掌握污染區域,並針對該區的污染源清查及減量,節省找出AMC污染源所需時間,防止污染區域擴大。
圖8、傳統出圖V.S.濃度分布圖
4.3.以動態濃度分布圖呈現污染改善
將每日濃度分布圖合成動態濃度分布圖,以每週動態方式,發布於網頁及Web-Mail檢視,如 圖9所示。當AMC發生異常時,可快速了解廠區AMC濃度分布情形及每日復歸情況,並可作為定期檢討及改善追蹤方向的依據。
圖9、每週動態分布圖

4.4.視覺化管理方式
傳統的AMC管理上,往往當無塵室有異常警報觸發時,才進行異常區域的查漏及狀況排除,常常緩不濟急。若是能在平日各區濃度維持在正常的濃度標準間,一旦發現該區讀值有偏高狀態,立即進行污染源清查及改善,便能避免污染擴大。
AMC濃度分布圖透過每日Web-Mail的寄送提醒,讓Module清楚了解無塵室各區AMC分布狀況,面對AMC讀值較偏高的區域,Module成立專案團隊,及早進行機台漏點查詢及改善,如 圖10所示,共同維護無塵室內環境品質,將AMC預防勝於治療落實在無塵室環境中。
圖10、視覺化管理方式

4.5.利用濃度分布圖改善環境實例
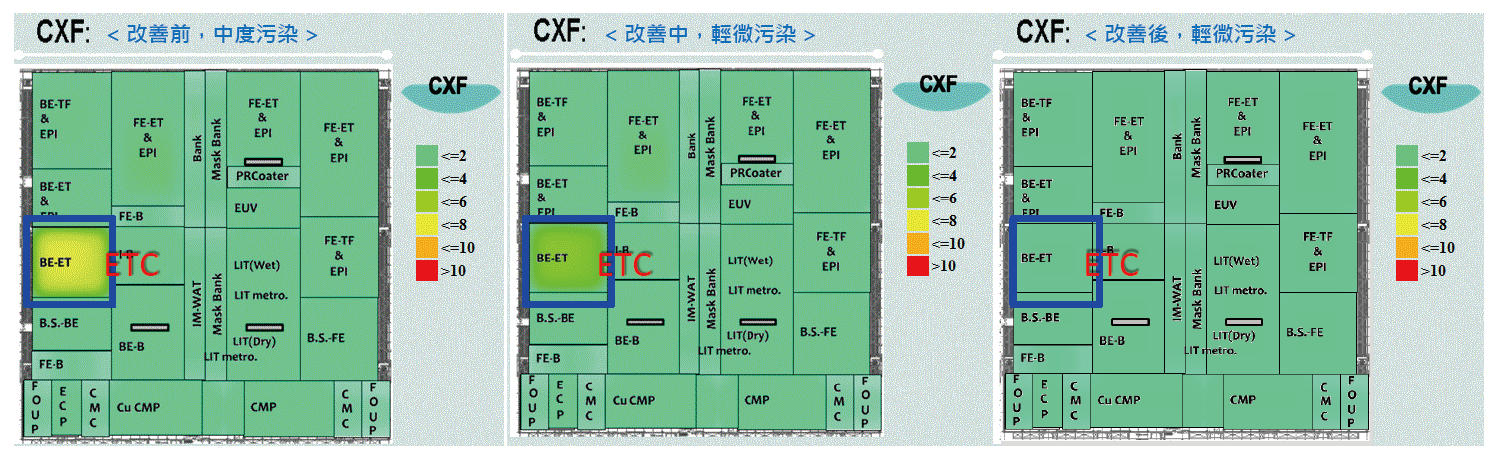
以蝕刻區為例,該區在濃度分布圖上呈現中度污染狀態(黃色),當濃度分布圖Mail發送後,優先進行該區全面調查,經確認漏源及改善後,濃度分布圖已回復至良好狀態(綠色),如 圖11所示。
圖11、蝕刻區域污染改善
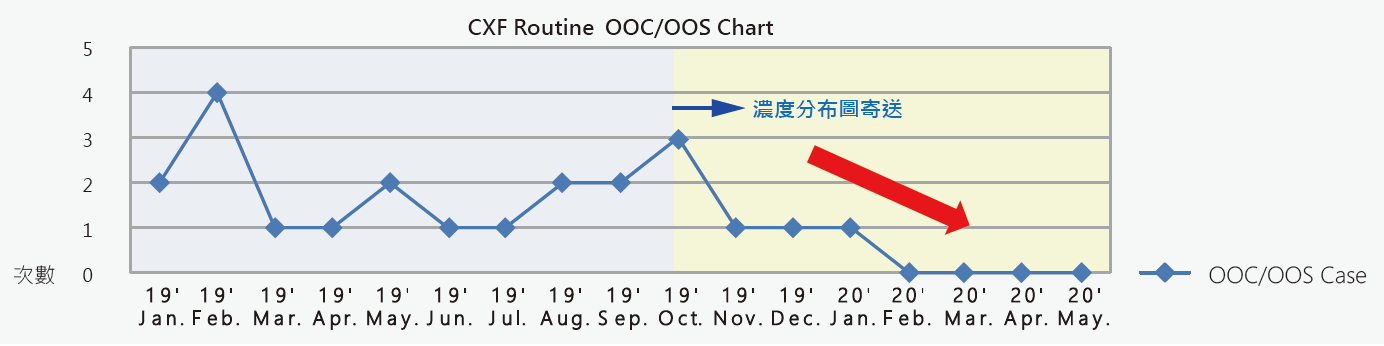
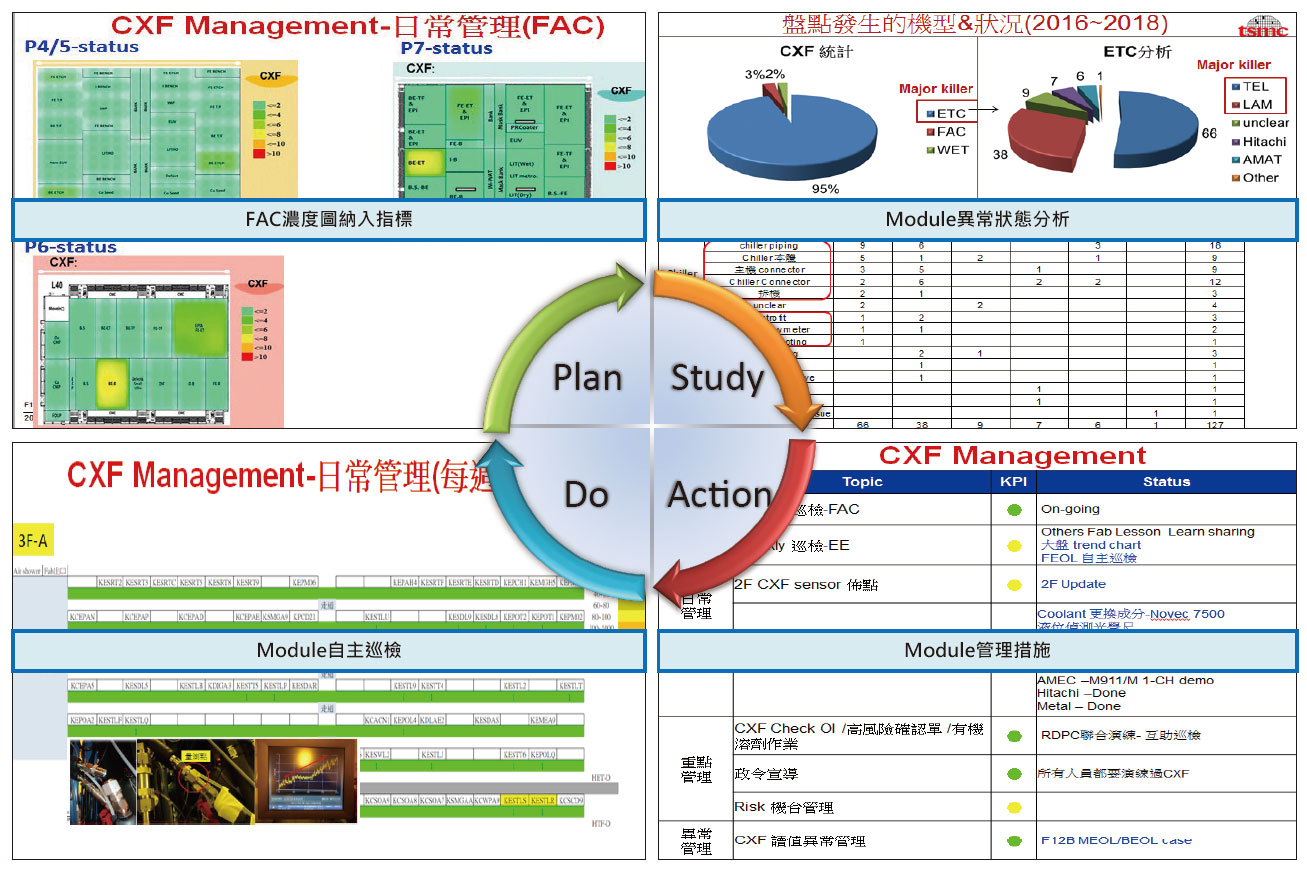
自濃度分布圖發送後,廠區OOC/OOS案件呈現明顯下降趨勢,由2~3次/月降至1次/2個月,如 圖12所示。每當有區域濃度偏高時,蝕刻Module人員立即成立專案管理,將其納入每週改善指標,視機台洩漏造成生產環境污染為改善項目之一,並藉由異常設備進行異常分析,訂定設備管理方案,每週自主巡檢檢查,發現問題,立即改善,如 圖13所示,使FAC與Module在環境維護上能共互助合作,達到良好的生產環境。
圖12、CFX OOC/OOS Case

圖13、Module成立專案管理
4.6.未來系統發展與改善
目前的AMC污染監控模式,為取樣管路佈點方式,皆為固定偵測方式,無法於無塵室內隨處移動監控,實際數據不足處仍需人員協助巡檢點的量測。未來的AMC污染監控模式,將AMC監測儀器裝載至自動導向車AGV結合IOT無線傳輸系統,可於無塵室內隨處移動監控,具有自動巡檢及智慧監控等功能。隨著量測點的增加,可將濃度分布地圖更臻於完善。
另外,在網頁輸出功能部份,將增加下列三項功能,如 圖14所示 :
圖14、網頁新增功能呈現
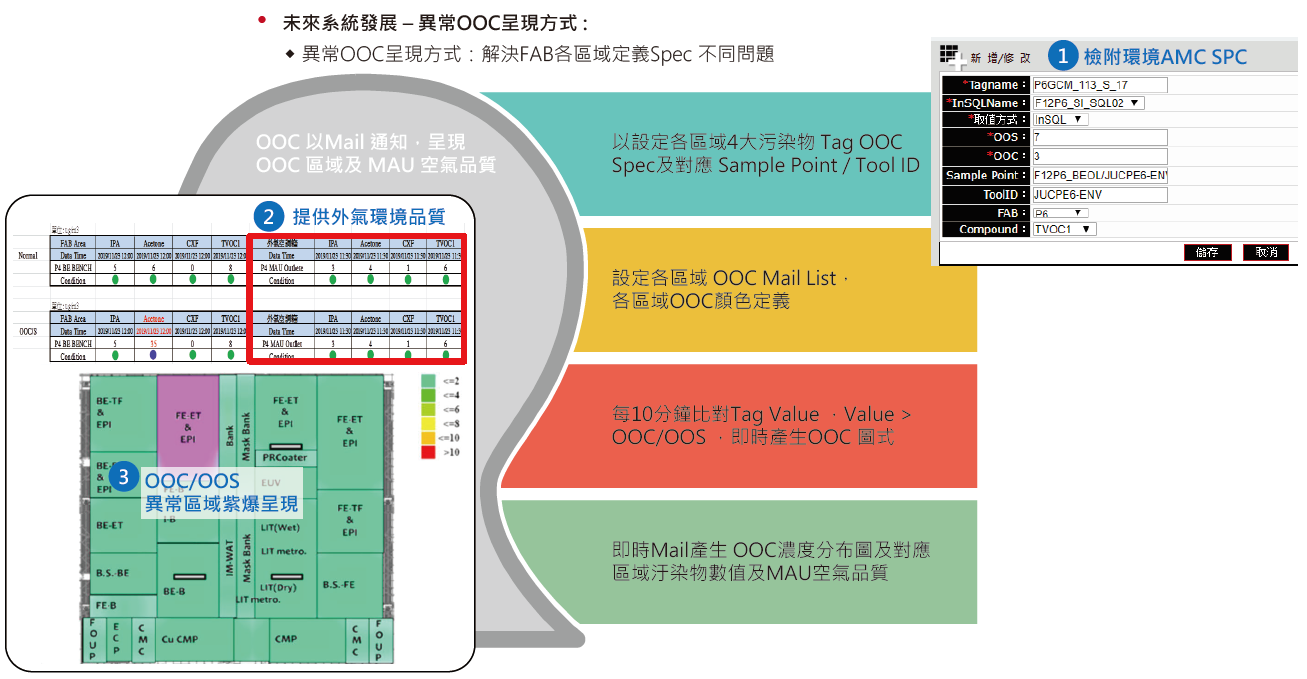
- 檢附環境AMC Spec : 可輸入無塵室各區環境OOC/OOS Spec,解決FAB內各區定義Spec不同問題。
- 提供外氣環境品質 : 增設外氣(MAU無塵室供應端)AMC濃度燈號,讓外氣狀態一目了然。
- 異常區域紫爆呈現 : AMC異常事件發生時,將該區紫爆呈現,並結合實驗室Mail發送功能,將外氣AMC濃度燈號與無塵室內濃度分布圖同時寄送,可直接辨別供應端狀態是否正常。
結論
有別於傳統濃度曲線圖表示方式,AMC濃度分布圖採用2D多色澤的視覺化效果,將同種物質濃度以顏色分層方式能讓人快速辨別差異,清楚呈現無塵室內部各區域的AMC濃度狀態。當污染物發生的同時,可快速掌握污染區域,針對該區的污染源清查及減量,提高管理決策之優先性,防止污染區域擴大。此外,濃度分布圖除了用於AMC呈現外,也可用於溫溼度/PA檢測等圖面效果呈現。
既有的AMC管理模式,屬於被動處理且單方面查漏運作方式,當無塵區異常濃度觸發警報時,需由人員點擊各區資料庫的濃度曲線,局部了解該區污染狀態後,由FAC單方面搜尋污染源及後續相關改善措施;透過AMC視覺化管理模式,採取主動預防且雙方面查漏運作方式,藉由廠區每日濃布圖Mail發送提醒,可全覽無塵室全區狀態,當無塵區濃度偏高時 ,由Module及FAC人員共同協助漏源改善及預防措施。
參考文獻
- 曾昭衡,「室內空氣品質監測及空氣污染地圖研究」,台灣室內空氣品質淨化博覽會,2019。
- Jin Li, Andrew D. Heap., Spatial interpolation method applied in the environmental sciences: A review. (2014)
- 計算流體力學簡介 http://www.mheducation.asia/olc/cengel
- 柯伯政,「以反距離權重法擴散PM2.5繪製空污地圖」,靜宜大學,2018。
- 施明倫,「結合監督模式與共克利金法估算河川污染指標面化圖 」,航測及遙測學刊,2013。
- Chen, F.W, Liu, C.W., Estimation of the spatial rainfall distribution using inverse distance weighting(IDW)in the middle of Taiwan. (2012)
- SHEPARD,D., A two-dimensional interpolation function for irregularly-spaced data. (1968)
- 溫欣儀,「通用克利金法的統計結構模型選擇和參數檢定方法」 ,台灣大學。
- 陳勝全,「以空間內插法分析崩塌地崩塌量體之研究」,國立中興大學。


留言(0)