摘要

潔淨室氣態分子污染物(AMC)污染源之預測方法
一般潔淨室設計中對於汙染源的預測大多採取由已知點釋放汙染物(實驗或計算),再觀察汙染源擴散的情況的方式來瞭解汙染物在潔淨室中的行為。但在真實運轉中的潔淨室,通常我們只能觀測到結果,而無法得悉汙染物由何處而來,若擬求解此類工程問題一般採取「逆方法」運算求解。本研究採用「以機率法為基礎」的計算流體力學逆方法估算一座二維潔淨室內的汙染源,並比對原先採取正向計算的結果。本研究所獲得的結果顯示所預測最有可能成為汙染源的位置與機率與正向計算的結果相符。
前言
對於許多密閉環境如潔淨室或機艙而言,若發現有污染物時,在不考慮有其它來自外界的持續性污染源為前提下,只要能夠尋找到污染源,通常能夠有效的針對污染加以防治,但對於實際上所遇到關於污染擴散的問題而言幾乎都只能觀測到結果,從而大部分污染擴散問題只能做到治標而不能治本。因此,從求解物理量的觀點而言,只要其描述問題的統御方程式在已知的邊界條件及起始條件下存在唯一解,這種主要描述及求解物理模型的「因~果」關係,一般稱為正向求解問題(Well-pose problem)。相反的倘若要由已知結果以有限的資訊(如污染物的分佈以及氣流形態)求解「因」,從數學的觀點則稱為「病態」問題(Ill-posed problem);而求解的方法則稱為逆向求解模式(Inverse method)。由於對密閉空間而言,污染物的分佈以及氣流形態是可以偵測得到的,倘若我們把這些量測得到的數據當作起始及邊界條件,透過逆向求解輸送方程式,推算污染源起點及強度是可能的。因此,本研究有別於一般採用傳統正向求解方式,擬透過逆向求解模式估算在潔淨室的汙染源分布為已知的情況下,預估汙染源的可能位置,作為潔淨室內汙染防治的手段。
文獻回顧
基本上逆向求解模式一般分為邊界型問題、重建型(時間反演)問題、係數問題及幾何型問題。邊界型問題為從已知結果倒推原來的邊界條件,重建型(時間反演)問題則為從已知結果倒推原來的起始條件。係數問題是根據已知結果倒推推求統御方程式內係數(例如污染輸送方程式的係數),至於幾何型問題則為由結果反推原有計算區域的幾何形狀。不過要注意在實際計算時因為不同的「因」將會導致不同的「果」,換言之,解有可能不為唯一。更何況此問題為Ill-posed,故求解的過程容易產生不穩定性。在實際物理世界中,因為時間是不可逆的,因此逆向過程無法以時間驗證,故解的正確性不易被驗證。
處理逆向問題的方法可分為「解析法」、「最佳化法」、「直接法」以及「機率法」等。「解析法」已在熱傳遞、地下水及一維污染輸送問題上已有所斬獲,但僅能求解簡單的問題,故採用此方法在實際運用上很有限。「最佳化法」是將所有可能的「因」以正向求解的方式得到一組答案,再與實測的數據以擬合的方式來得到較佳的答案;這些方法包括了「線性最佳化法」、「最大相似法」,以及「非線性最佳化法」。「直接法」為直接逆向求解統學御方程式來描述其因果關係,但是求解方程式的過程本身是不穩定的。在處理空氣汙染擴散類型的題目中,例如由Zhang and Chen[1]所提出的「準可逆法」(Quasi-Reversible Method),屬於直接法的一種,它直接求解統御方程式,但為防止求解過程中發生不穩定的現象,運用了一些穩定性技巧修改了容易造成不穩定的項,成為類似原統御方程式的型式並加以取代、求解。準可逆法以成功的運用在熱傳導問題及地下水污染源預測問題上。不過,「準可逆法」需要相當準確的速度及濃度場資料,否則即有可能導出錯誤的結果。其次在「準可逆法」中其擴散項在離散化後,在「負」的time-step增時為了讓運算過程穩定,增加了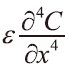 這個「人造」的擴散項以防止計算發散,如此一來便與原始物理模型有所出入,因此逆向求解的方法若能與原有的物理模型或定義相符,便更能真實體現逆方法的可用性。Neupauer and Wilson[2][3]所採用以原有物理模型來計算各種可能結果「出現機率」的方式,這種方式可稱為所謂的「機率法」。機率法在概念上是搭配許多可能的「果」,透過逆向求解來得到「因」,再以機率的觀點探討每個解出現的可能性。這種方法雖然在直觀上不易被理解,而且針對複雜的情況需開發新的演算法,但是這種方法一次僅依其「事件發生」的可能性計算一個可能的解,而且「事件」僅需少許的變數即可展開反向計算,倘若需提高計算精度(即出現機率)只需增加可能的「事件」出現次數即可。因此本方法不像「準可逆法」需要套用「人造」的擴散項須大幅修改離散方程式,只要利用現有的計算流體力軟體套用即可,其精度可軟體套用即可,其精度可藉增加偵測點數量來改善,因此較容易切入研究主題。
這個「人造」的擴散項以防止計算發散,如此一來便與原始物理模型有所出入,因此逆向求解的方法若能與原有的物理模型或定義相符,便更能真實體現逆方法的可用性。Neupauer and Wilson[2][3]所採用以原有物理模型來計算各種可能結果「出現機率」的方式,這種方式可稱為所謂的「機率法」。機率法在概念上是搭配許多可能的「果」,透過逆向求解來得到「因」,再以機率的觀點探討每個解出現的可能性。這種方法雖然在直觀上不易被理解,而且針對複雜的情況需開發新的演算法,但是這種方法一次僅依其「事件發生」的可能性計算一個可能的解,而且「事件」僅需少許的變數即可展開反向計算,倘若需提高計算精度(即出現機率)只需增加可能的「事件」出現次數即可。因此本方法不像「準可逆法」需要套用「人造」的擴散項須大幅修改離散方程式,只要利用現有的計算流體力軟體套用即可,其精度可軟體套用即可,其精度可藉增加偵測點數量來改善,因此較容易切入研究主題。
由於本研究旨在運用逆方式,由已知潔淨室的污染的位置及強度,反推可能的污染物發生源。因此在檢討過上述方法後,發現機率法只需要少許資訊(如物理通量、釋放時間及偵測點)以及花費少許運算時間便可計算,因此本研究將採用「以機率法為基礎」的逆運算法作為處理逆向問題的計算模式。
計畫
由於「以機率法為基礎」的逆方法在物理直觀上比較難理解,因此在本節先介紹本方法的概念與原理,其次再說明本方法的物理架構及實際的計算方法,茲以下例作為說明:
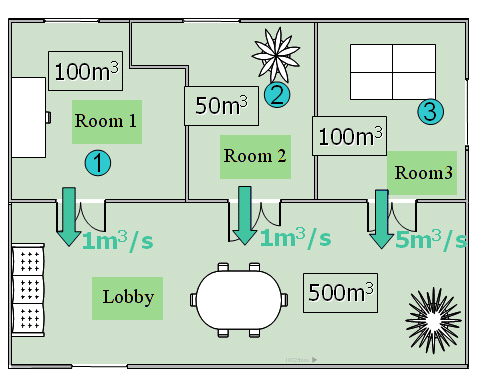
若考慮一座居室布置如圖一所示,若於室內某處釋放XV神經毒氣1g,並假定於10sec後分別於第一室、第二室與第三室測得的質量分別為0.1g、0.2g以及0.5g。因此在時間t=T>0的時間之後,對於某個監測點Xo,i所量到的毒氣質量,可能來自於該毒氣釋放源Xs,i的機率稱之為正向位置機率(Forward location probability, FLP),可用下式表示:
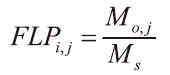
圖一、居室布置圖
但在實際上我們並不能確認毒氣必然來自於FLP中所預測的位置,因此我們不能肯定的說該點必然來自於Xs,i,而只能說「來自於Xs,i的可能性」,也就是指來自於Xs,i的「機率」。因此若該某個監測點Xo,i所量到的毒氣來自於毒氣釋放源Xs,i的可能性,我們就稱為反向位置機率(Backward location probability, BLP),可用下式表示:
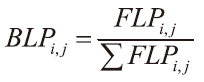
依據上述條件及定義,茲將各個房間的FLP與BLP列表如下:
在實際的問題上,毒氣可能是靠著氣流吹送到每一個房間,因此在考慮在某特定時間後,由不同氣流量傳送毒氣進入各個房間的濃度以及FLP可以表示如下:
由上述可知,若要計算FLP首先必須計算得到正向流場,也就是氣流以真實情況流動運動了若干時間(t=T>0)。由於在真實流場中我們可以偵測到污染物的濃度(雖然我們並不確定它來自何處?),接下來只要令原有的流場反轉,然後將所偵測點所量到的毒氣濃度以及位置當作起始的源點(Source),接著計算此一毒氣沿反轉的氣流留向可能的的位置而時間長度則為T,如此便能求到一「可能的」原始供應點,這樣就求得一個FLP;因此,便可進一步的推算每一個偵測到污染源其可能來自空間中任一點可能的「機率」(即BLP)。
|
MS=1g VX Gas at |
R1 |
R2 |
R3 |
|---|---|---|---|
|
Observed Mo in Lobby after 10s |
1g/100m3×1m3/S×10s = 0.1g |
1g/50m3×1m3/S×10s = 0.2g |
1g/100m3×5m3/S×10s = 0.5g |
|
FLP |
0.1g/1g = 10% |
0.2g/1g=20% |
0.5g/1g=50% |
|
BLP |
10%/(10+20+50)% = 12.5% |
20%/(10+20+50)% = 25% |
50%/(10+20+50)% = 62.5% |
|
MS=1g VX Gas at Lobby (obs) |
R1 |
R2 |
R3 |
|---|---|---|---|
|
Received mass after 10s at room |
1g/500m3×1m3/S×10s = 0.02g |
1g/500m3×1m3/S×10s = 0.02g |
1g/500m3×1m3/S×10s = 0.02g |
|
VX concentration after 10s at room |
0.02g/100m3 = 0.0002g/m3 |
0.02g/50m3 = 0.0004g/m3 |
0.1g/100m3 = 0.001g/m3 |
|
FLPi,obs = Ci×Volobs/Ms |
0.0002g/m3×500m3/1g = 10% |
0.0004g/m3×500m3/1g = 20% |
0.001g/m3×500m3/1g = 50% |
依據上述以「對流」及「擴散」的物理機制,本研究採用由Liu & Zhai[4]所開發以「機率法」為基礎的運算模式。
考慮如下的污染物濃度輸送方程式如下:
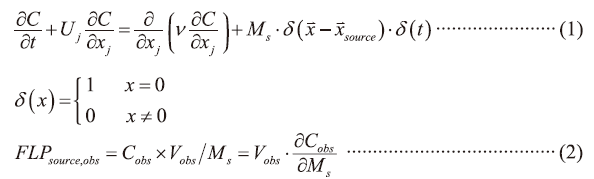
若(1)對Ms微分(即求FLP),則(1)式可改寫如下
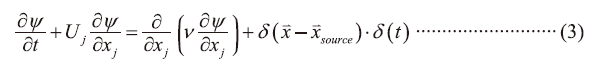
其中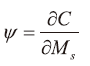
為了求解ψ,我們先將(1)式再改寫如下(即Forward equation)
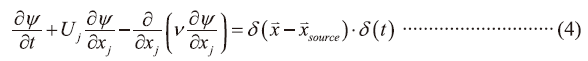
接著再考慮一組「自洽方程式」(Adjoint equation)如下
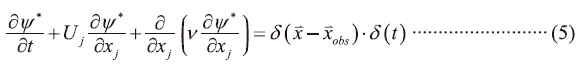
接著將可以得到Forward Eq.xψ+Adjoint Eq.xψ:可以得到
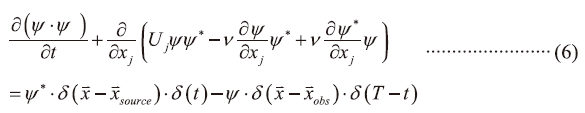
接著對整個流場及時間區域(即(6)式)作積分
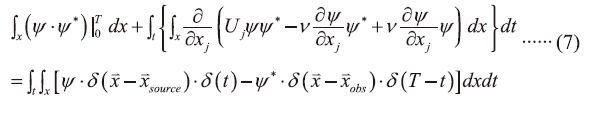
在上式第一項中若 ψ|0=0以及ψ*|T=0 ,則
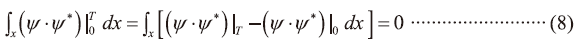
同時,若
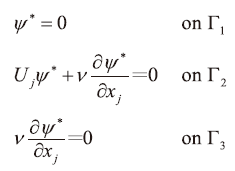
則可得到第二項
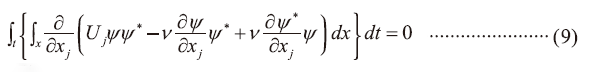
如此(7)式顯然可以得到
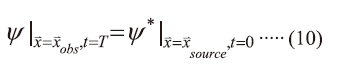
(7)式的物理意義即為來自各源點的皆有可能抵達某一觀查點,而由此觀察點也可以回溯到各可能的來源點,如圖二所示。
圖二、來源點與觀查點之正逆向關係
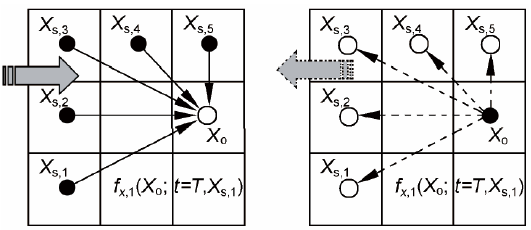
原有的(5)式(即「自洽方程式」)若考慮「時間反衍」,也就是從已偵側到污染物的時間T,反推回原來污染物釋放的時間原點,因時間無法以遞減方式前進(即時間的計算不能「負」的時間),因此我們考慮以t=T-t取代T,以確保計算時間仍為正,但(5)式則改寫為
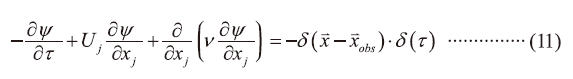
從而我們可以得到
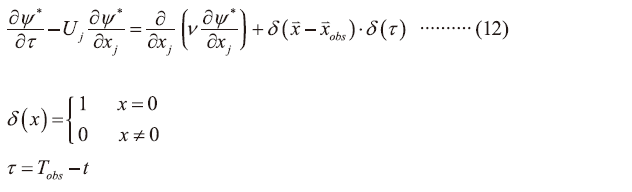
從而FLP便可求得
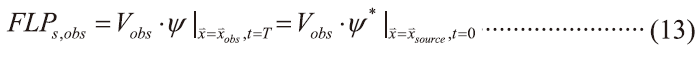
以目前本研究所要分析的問題,屬於多重偵測點(X*s,1 , X*s,2 ,...X*s,n)、已知擴散時間的條件性ALP問題;因此對空間中多重偵測點的情況下,空間中每一點為「可能」污染發生源之一組可能濃度分布為ψ*s,1 , ψ*s,12 ,...ψ*s,n,因此其「可能」污染發生源機率ψ之組合應為

其中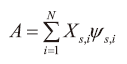
(14)式表示多重偵測點條件下,空間某特定點成為污染源的機率為該「特定點」為各個單一偵測點成為污染源機率的加權過的總和。其物理概念為以潔淨室的流場流型(Flow Pattern)以及強對流條件考量,每一次內部的潔淨循環氣流幾乎呈現相同的流線(Streamline),倘若多重偵測點中某一點呈現出最大的數值,代表該區成為污染源的可能性高,但也不能乎略其它偵測點所量測到較小數值。因此,對於各偵測點所得到的濃度以「權重」的方式可能分部進行疊加,而這種方法稱為「加權機率疊加模式」。
本研究透過二維的潔淨室模型,來驗證本方法的可用性。首先依其外形建立物理計算網格,接著依據上述的計算方法,必須先產生一正向流場後,再反轉流場並以偵測點當作污染源,觀測污染物「循原路返回」的情況來求得每一偵測點所推得的污染源機率分布。本研究利用熱流分析軟體FLUENT計算三維暫態之歐拉守恆方程式(Eulerian conservation equation)計算「正向」流場以及「反向」的污染擴散;流場可用以下方程式來加以描述

其中Φ代表每速度分量(u , v , w),紊流動能(turbulence kinetic energy, k),紊流動能耗散(dissipation rate of the turbulence kinetic energy, ε)以及物種(species mi'), ΓΦ則為每一變數Φ之有效交換係數(傳遞係數), SΦ代表源項。
求解多種純量場(Multi Specious,如污染物濃度等)如以下張量表示:
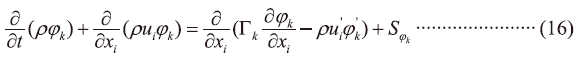
其中k=1,....,N,N為物種項目。
為求解紊流動能(k)紊流動能消散量(ε),以及純量擴散的漲落量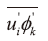 ,一般採用Two-equation模式(即標準k-ε模式)對紊流場求解出速度,並同時對本研究之其它擬分析之物理量求解。
,一般採用Two-equation模式(即標準k-ε模式)對紊流場求解出速度,並同時對本研究之其它擬分析之物理量求解。
依據上述計算得到FLP(ψ )之後,本研究將空間區域分割為i×j的區劃(即為i×j的矩陣),先計算各個區劃內的無因次濃度(也就是ψ*值),接著就可以計算多個偵測點所推求到不同的ψ*。若考慮在二維空間有偵測點A與B,若考慮A偵測點所得到的ALP為ψ*,偵測點B所得到的ALP為ψ*,其偵測點的濃度分別為Xs,1 ,Xs,2,因此疊和後的機率ψ表示如下

其中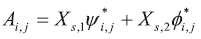
ψ*與Φ*的機率分布需各別對流場以計算流體力學方法求解(12)式後,建立與ψ*與Φ*的機率矩陣後,再帶入(17)計算便可得到「權重加總」後的機率矩陣。
結果與分析
為避免空間過大稀釋了濃度分布,導致結果難以觀測及計算機率分布,因此我們以計算小區域驗證潔淨室內可能污染源的位置,以驗證理論的證確性。本研究先考慮「小型」潔淨室如所示寬7.8m、寬3.6m的潔淨室立面。該潔淨室鋪設17%開孔率的高架地板,其高度自地坪起算為1.6m;高架地板到天花板的距離為3m,其FFU之覆蓋率為50%。計算以甲苯模擬氣態分子污染物(AMC),並假定污染物於機台與潔淨室的壓差為0.015Pa的情況下以10ppm連續洩漏至潔淨室內。此外,潔淨室的排氣以0.025m/s的速度排氣至外界。
由前述的理論中,我們也瞭解偵測點選用越多,理論上推估的空間中特定位置發生機率也會越高,從而提高其準確性,因此本研究採用了八個偵測點來量測間中污染物的濃度。為了建立機率矩陣,我們將計算空間分割為X×Y=10×10的矩陣,分別建立八個偵測點所形成的機率矩陣。我們先產生一組正向流場的解,作為產生逆向解的起始條件,以及作為與逆方法所求得的污染源之對照。作為「對照組」的濃度場正向運算分布如圖三所示,接著建立其反向流場。由於本流場性質接近「週期性」的流場形態,因此先行決定偵測點的取樣時間,若我們選取洩漏機台下方三點可以發現,在一週期內的50Sec左右時各點均可量測到最大濃度數,因此本研究將取50Sec作為污染物濃度取樣的時間點。各偵測點位置及濃度如表一所示。
|
偵測點1 |
偵測點2 |
偵測點3 |
偵測點4 |
偵測點5 |
偵測點6 |
偵測點7 |
偵測點8 |
|
|---|---|---|---|---|---|---|---|---|
|
座標 |
Xmin=2.1m, Xmax=2.6m |
Xmin=3m, Xmax=3.5m |
Xmin=3.9m, Xmax=4.4m |
Xmin=4.8m, Xmax=5.3m |
Xmin=5.7m, Xmax=6.2m |
Xmin=6.6m, Xmax=7.1m |
Xmin=7.5m, Xmax=8m |
Xmin=8.4m, Xmax=8.9m |
|
Ymin=1.1m Ymax=1.5m |
Ymin=1.1m Ymax=1.5m |
Ymin=1.1m Ymax=1.5m |
Ymin=1.1m Ymax=1.5m |
Ymin=1.1m Ymax=1.5m |
Ymin=1.1m Ymax=1.5m |
Ymin=1.1m Ymax=1.5m |
Ymin=1.1m Ymax=1.5m |
|
|
濃度 |
3.116183 |
28.48624 |
22.31855 |
10.4027 |
1.326601 |
0.038636 |
0.009083 |
0.000801 |
圖三、計算流場偵測點位置(左)及濃度的正向解(右)
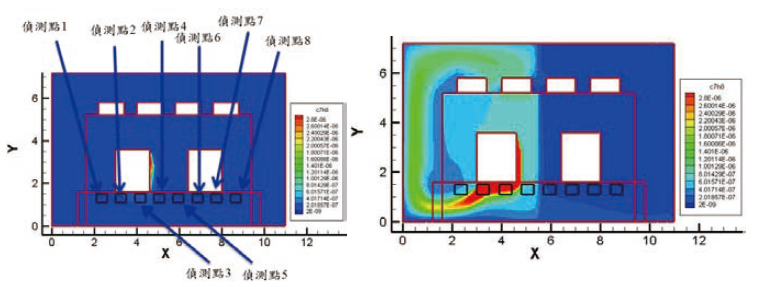
依據上述正向流場的解將流場反向後,作為氣流的起始條件,再以各別8個偵測點(Xs,1 , Xs,2 , ...Xs,8)分別作為新流場的污染源進行釋放,所求得的污染物濃度分布以及機率分布如圖四至圖十一所示。
圖四、第1偵測點所讀取濃度及逆方法計算之濃度分布
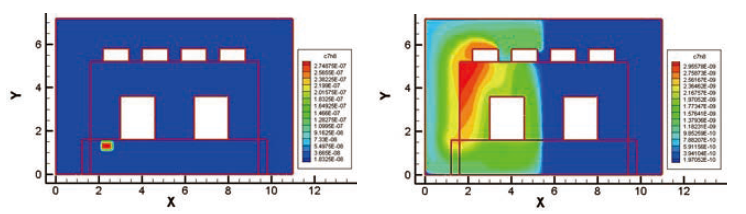
圖五、第2偵測點所讀取濃度及逆方法計算之濃度分布
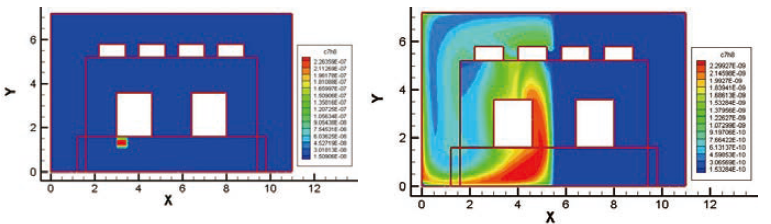
圖六、第3偵測點所讀取濃度及逆方法計算之濃度分布
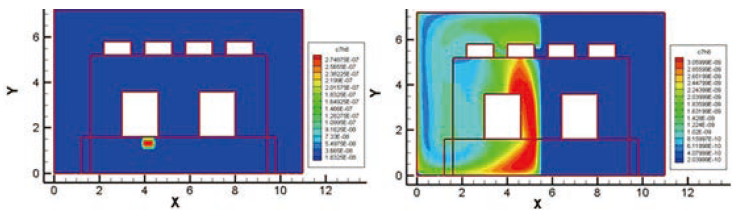
圖七、第4偵測點所讀取濃度及逆方法計算之濃度分布
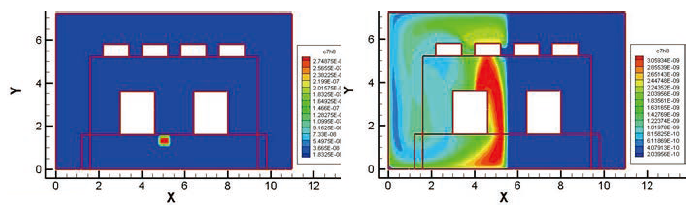
圖八、第5偵測點所讀取濃度及逆方法計算之濃度分布
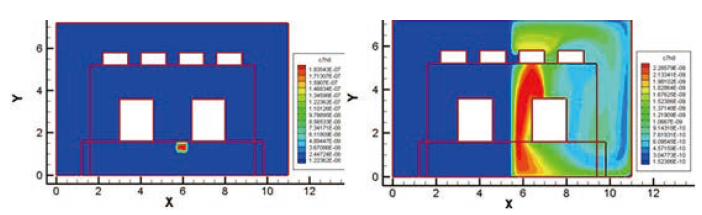
圖九、第6偵測點所讀取濃度及逆方法計算之濃度分布
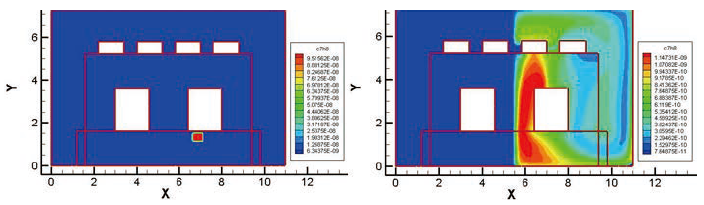
圖十、第7偵測點所讀取濃度及逆方法計算之濃度分布
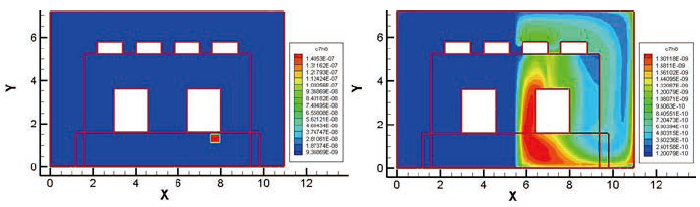
圖十一、第8偵測點所讀取濃度及逆方法計算之濃度分布
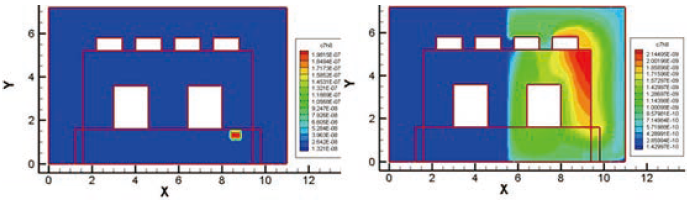
由於潔淨室的強對流條件,使得污染物的擴散大多侷限在左潔淨室的左側或右側(視來源決定)。依據Zhai[4]的計算方式,空間某特定點成為污染源的機率為該「特定點」為各個單一偵測點成為污染源機率的疊合。假定由A偵測點經逆運算所得到污染源機率為曲面A,而由B偵測點經逆運算所得到污染源機率為曲面B,因此將兩曲面疊和(相乘)即代表其各事件(Event,即分別為A與B偵測點)的機率疊合,其機率相乘數值最高部份即為最大可能發生的位置。基本上若偵測點越多,其疊和後所計算得到的發生機率也會提高。不過該方法考慮氣流可能通過空間中所有的路徑,與潔淨室「循環且對稱」的氣流流形是不符的,倘若採該方式會發生機率疊和結果為零的情況,特別是污染物在一側,偵測點在另一側的情況下。回顧表一所量測到的結果,可以發現潔淨室右側(第五至第八個)偵測點所量測之結果級值與左側的結果相差甚大,反而將影響疊合計算的結果,得出與事實不符的結果。因此必須設置一個過濾的機制,也就是「權重」的觀念強調高濃度量測值的計算結果,同時在不忽略低濃度量測值的計算結果而予以淡化。依據此觀念將八點疊加的計算結果如圖十二所示,其預測結果顯示最有可能成為流場污染源最高機率點的位置,與正向運算時污染物「確實」的釋放點一致(圖三右側)。
圖十二、所有偵測點(共八個)以逆方法運算可能污染源機率分布疊加之結果
同時,為確認此方法與選擇偵測點無關(但仍考慮權重),故再依據第1、3、5、7與第2、4、6、8點量測結果進行逆方法計算之結果分別疊加後所呈現與流場污染源最高機率點的位置幾乎為一致(圖十三、圖十四),因此確認偵測點位置選用的獨立性。
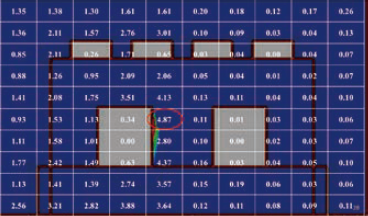
圖十三、第1、3、5、7偵測點以逆方法運算可能污染源機率分布疊加之結果

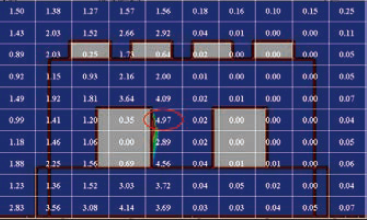
圖十四、第2、4、6、8偵測點以逆方法運算可能污染源機率分布疊加之結果
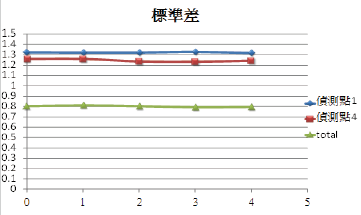
除此之外,本研究也對於逆方法預測之機率分布和汙染物數值濃度之間的「獨立性」進行檢討。本部份將就第1與第4個偵測點濃度分別為1以及10,000倍時進行重新以逆方法計算。第一點濃度提高為10以及10,000倍時的計算結果如圖十五及圖十六所示,而第四點實施相同計算時的結果如圖十七及圖十八所示。計算的結果顯示數值隨著級值略有漲落,但比例與位置不變,若取矩陣內前五高之數值計算其標準差,結果顯示變化極微,已落在工程設計上接受的範圍內(圖十九)。
圖十五、第1偵測點於釋放濃度提高10倍以逆方法運算可能污染源機率之結果(單位%)

圖十六、第1偵測點於釋放濃度提高10,000倍以逆方法運算可能污染源機率之結果(單位%)

圖十七、第4偵測點於釋放濃度提高10倍以逆方法運算可能污染源機率之結果(單位%)

圖十八、第4偵測點於釋放濃度提高10,000倍以逆方法運算可能污染源機率之結果(單位%)

圖十九、由第1及第4矩陣內前五高之數值求得之標準差
標準差的計算方式為:
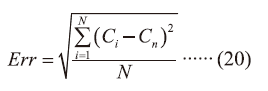
其中
Ci:目前濃度所測得濃度值
Cn:濃度的平均值
N:取樣點數
另外八點疊加後,即使濃度提高至10,000倍後,也呈現相同的計算結果(圖二十),說明本方法與釋放物濃度的高低無關。
圖二十、所有偵測點於釋放濃度提高10,000倍以逆方法運算可能污染源機率疊加後之結果(單位%)

結論
本研究透過「以機率法為基礎」的計算流體力學逆方法估算一座二維潔淨室內的汙染源位置,經由本研究目前分析結果可得到以下結論:
- 對於二維潔淨室污染源採用本研究所提出修正原先「以機率法為基礎」的「加權機率疊加模式」逆方法運算預測氣態污染源之結果,與先前潔淨室正向流場所訂定的污染源位置吻合。
- 採用「加權機率疊加模式」的逆方法運算結果不受偵測點的位置及污染物排放濃度的影響。
參考文獻
- T.F. Zhang, Q. Y. Chen,“Identification of conta-mination source in enclosed environment by inverse CFD method”, Indoor Air, Vol.1 , Issue 3, pp.167-177, 2007.
- R. M. Neupauer, J. L. Wilson,“Adjoint method for obtaining back-in-time location and travel time probabilities of a conservative gropundwater system”, Water Resource Research, Vol. 35, No.11, pp. 3389-3398, 1999.
- R. M. Neupauer, J. L. Wilson,“Adjoint-derived location and travel time probabilities for a multidimensional gropundwater system”, Water Resource Research, Vol. 37, No.6, pp. 1657-1668, 2001.
- X. Liu, Z. Zhai,“Location identification for indoor instantaneous point contaminant source by probability-based inverse Computational Fluid Dynamics modeling”, Indoor Air, Vol.18, pp.2–11, 2008.



留言(0)