創新綠色廠房跨廠區回收水網路節水構思

Introduction

In a semiconductor factory, water is one of the indispensable utility for several process operation. For example, water is essential for doing backside grinding on wafer, cleaning process tool, blowing down air contaminant in scrubber, serving as cooling medium to remove extra heat. Since the large amount of water consumption in semiconductor factory and the insufficient of water resource in recent years in Taiwan, Taiwan Semiconductor Manufacturing Company(TSMC) puts a lot of effort on enhancing water recycle rate in each fab. However, for the time being, the implementation of water recycle focuses on the scope in individual fab. This article aims to propose an inspiring concept to discuss the opportunities of inter-fab water recycle.

The possibilities of inter-fab water recycle is worth exploring, since several TSMC’s Fabs are situated in neighboring area in Hsinchu. Besides, the quality and quantity of effluent are different form Fab to Fab because of the difference in processes. The effluent which cannot be reused in a certain fab may have the potential to be reuse in another fab.

At present, several inner-fab Reuse City Water (RCW) tanks are established to store effluents for further reuse in each fab. These effluents may come from air washer drain, MAU/AHU condense, AWR reclaim effluent, LSS reclaim effluent and some other sources. The new concept discussing in this article is to install an inter-fab RCW tank in order to open the possibilities of inter-fab water reuse. This concept may be a helpful strategy to solve the water shortage problem.

Background

In academic research, the methodologies on water minimization can be generally classified into two broad categories: the graphical based pinch analysis (Wang and Smith, 1994a,b; Kuo and Smith, 1998) and the mathematical-model based optimization technique (Galan and Grossmann, 1998; Huang et al., 1999; Gunaratnam et al., 2005; Karuppiah and Grossmann, 2006). In addition, a new design manner with internal RCW tanks to simplify the network complexity and to improve the overall practicability was proposed (Feng and Seider, 2001; Wang et al., 2003; Zheng et al., 2006; Ma et al., 2007). More recently, Liu Y. Z.’s group (2008) presented a hybrid structure for the design of water networks, in which work the compromise between network complexity and freshwater requirement has been discussed. All of the above-mentioned works have focused on water integration within single fabs. In order to further enhance water recovery potential, inter-fab water integration should be taken into account (Olesen and Polley, 1996; Liao et al., 2007; Chew et al., 2008).

This article presents a general formulation for water integration within a production site, e.g. an industrial park of different fabs, or a process fab with operations grouped into different geographical locations according to the fab layout and/or processing tasks. Opportunities for the transfer of water between fabs (or, zones) are considered, and design options are fully incorporated in the formulation, so it serves as a base to apply various integration schemes. An illustrative example is provided to demonstrate the application of the proposed formulation.

Methodology

Problem Statement

Given is a total site with a set of plants. Each plant includes a set of water-using units where a set of transfer-able contaminants with fixed mass loads are required to remove. A set of freshwater supplies with known concentrations are available for service; a set of inner-plant and/or inter-plant water mains would be used to increase the network flexibility. The objective is to determine an optimal operating strategy for the inner-plant and inter-plant water integration scheme, which targets the minimum freshwater consumption and wastewater production.

Mathematical Formulation

Superstructures for processing equipments are built and shown in Figures 1-3, on which the mathematical formulation is based. In addition to the constraints to ensure design specifications and feasibility, the problem consists of water and contaminant balance equations. Following this, a general formulation is presented first, and then various integration schemes can be represented by imposing supplemental constraints appropriately.

Figure 1 depicts the superstructure of all possible flow connections for a water-using unit i, where the input water would come from other water-using units i', water mains m, and freshwater supplies w. Similarly, the output water may be sent to other water-using units i', water mains m, or receiving tanks r. According to the superstructure, the water and contaminant balances for each water-using unit can be derived as given in Eqs. (1)-(3) and Eqs. (4)-(7), respectively. Note that c is the index for contaminants.

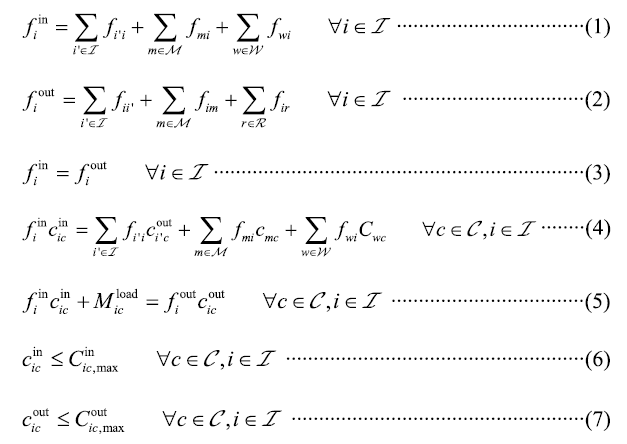
Figure 1. Superstructure for a water-using unit

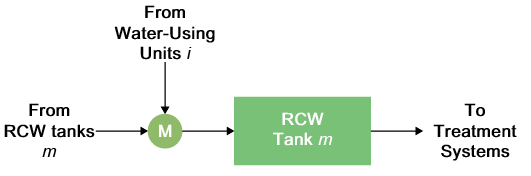
Figure 2 depicts the superstructure of all possible flow connections for a RCW tank m, where the input water may come from water-using units i, other RCW tanks m', and freshwater supplies w. Meanwhile, the output water may be sent to water-using units i, other RCW tanks m', or receiving tanks r. RCW tanks would be distributed to individual fabs (zones), or centralized, whose purpose is to simplify the overall network complexity. In accordance with this superstructure, the water and contaminant balances are derived in Eqs. (8)-(10) and Eq. (11), respectively.

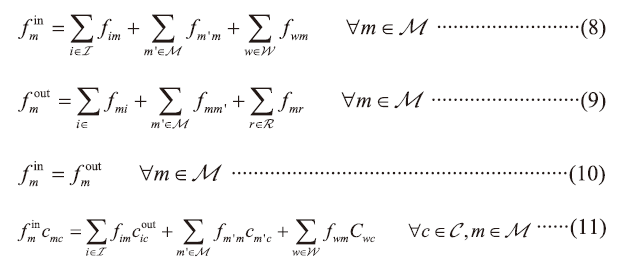
Figure 2. Superstructure for a RCW tank

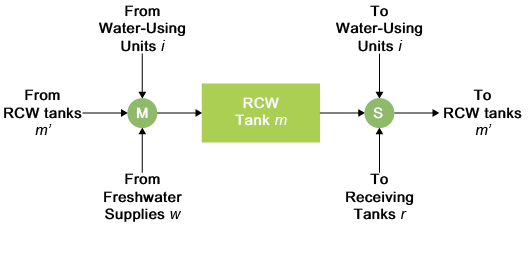
Figure 3 shows the superstructure for a receiving tank, like a buffer where the wastewater is held before being sent to treatment systems. The water balance for each receiving tank is given in Eq. (12). It is worthy of mention that effluent treatment is quite important for environmental concern, but this part is omitted and kept for future work

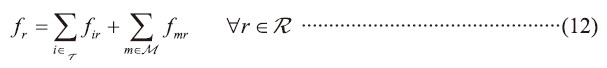
Figure 3. Superstructure for a receiving tank

Equation (13) defines the lower and upper limits to the connecting flow rates with the use of binary variables. y*=1 denotes the existence of the connection between *.

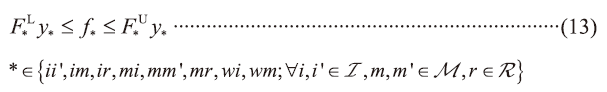
So far, the aforementioned equations constitute a basis for inter-fab water integration, as a general case of hybid design options. For convenience, the equations are grouped to a set Ω0≡{Equations (1)-(13)}. Five integration schemes are considered in this work, as described below: (Note: IPI =inter-fab integration; p=index for fabs; Mcen and Mcen are sets of centralized and inner-fab mains).

• Case 1: No IPI without using RCW tanks:
  
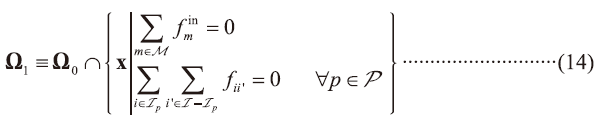
• Case 2: No IPI with inner-fab RCW tanks
  
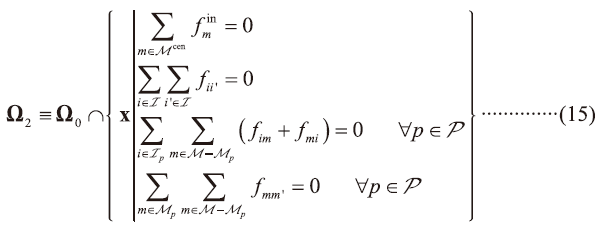
•  Case 3: direct IPI (Chew et al., 2008)
  
•  Case 4: indirect IPI (Chew et al., 2008)
  
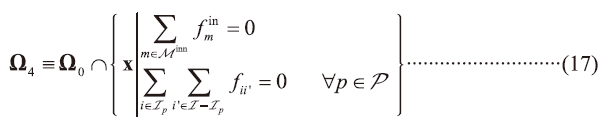
• Case 5: IPI with centralized/inner-fab RCW tanks, without the use of cross-fab pipeline
  

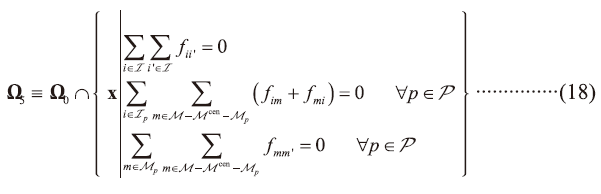
Finally, the objective shown in Eq. (19) is to minimize the freshwater consumption. Besides, the design problem is a mixed-integer nonlinear program (MINLP) for the binary variables and bilinear terms.

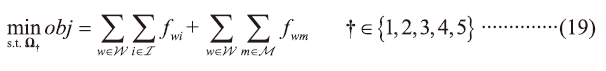
Results

The example with fifteen water-using units divided into three individual fabs (each adapted from Wang et al., 2003, Example 2; Zheng et al., 2006, Case study 2; and Gunaratnam et al., 2005, Case study 1) is provided to illustrate the application of the proposed formulation. The solution tool is the General Algebraic Modeling System (GAMS, Brooke et al., 2003), and the solver for MINLP is BARON.

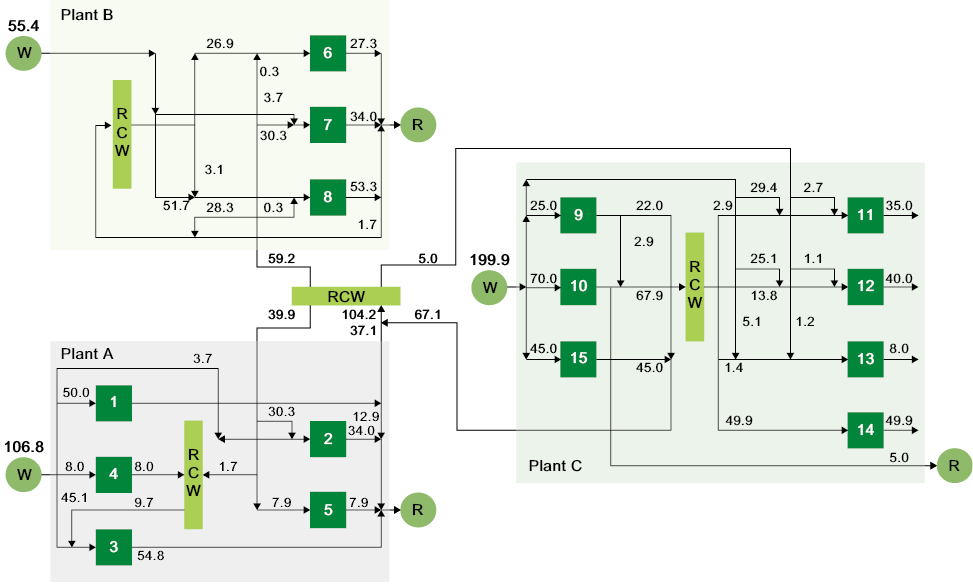
In case 1, without any inter-fab integration, the respective freshwater consumptions of individual fabs are 111.81 ton/h, 111.83 ton/h and 183.59 ton/h, with a total amount of 407.24 ton/h. In case 2, inner-fab RCW tanks are put in each fab to enhance the operability, but the mixing effect increases the overall freshwater consumption from 407.24 ton/h to 421.82 ton/h. In case 3, direct IPI is carried out and the overall freshwater consumption is reduced from 407.24 ton/h to 354.46 ton/h in comparison with case 1. However, direct IPI would be hard to operate for control problems and the network complexity. Therefore, indirect IPI is performed in case 4. Although the overall freshwater consumption is slightly increased to 355.54 ton/h because of the mixing effect, the network structure will be simpler. For some larger scale problems, centralized RCW tanks would be employed in addition to inner-fab mains for practical needs so case 5 is to be examined. The freshwater consumption is slightly increased to 362.1, but the operability of the whole fab can be improved when compared to cases 3 and 4. The resultant network configurations for cases 2 and 5 are shown in Figs. 4 and 5, respectively.

Figure 4. Resultant network configuration for case 2

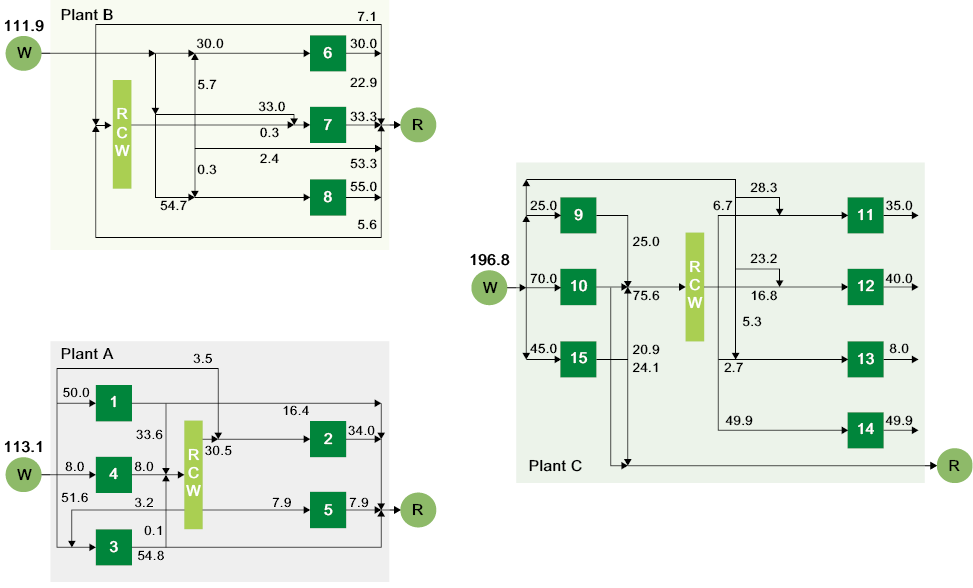
Figure 5. Resultant network configuration for case 5

Conclusion

A general formulation for inter-fab water integration has been developed in this article. Five integration schemes were considered with the objective to minimize the freshwater consumption, and an illustrative example was solved to demonstrate the validness of the proposed MINLP formulation. In future work, treatment units for regeneration and effluent treatment will be combined into the inter-fab design problem, and the objective will be turned to minimize the total annual cost (TAC) for cost-effective operation. A further advantage of discussing the possibility of installing inter-fab treatment unit is to reduce the capital cost of treatment unit by sharing it in central area. Moreover, sharing the treatment units can save the space in each fab.