摘要

壓力驅動的網管流模擬
Keywords / Netted Piping Or Tubing Flow,Steady State,Unsteady State,Isothermal,Adiabatic2,Equation Of State
常見流體在單管中的流動,在網管間的流動甚少提及。本研究以壓力、質量流率、比容及焓做為計算變數,並引入狀態方程式以計算非理想氣體的流動。以節點做為質量及能量守恆的條件,不需要有封閉回路或虛擬回路。由於園區氣體在管路中流動,速度大小限制在25公尺以下,因此流動可視為不可壓縮流,為方便及簡化計算,假設流體元件不堆積質量。透過質量、動量及全能守恆得有數學模式,即可進行複雜地求解。此研究的數學模式,分等溫、絕熱、穩定態及非穩定態。由於不見氣體網管流的經典比對範例,因此在氣體流動的比對,採用氣體單管絕熱流動範例;在液體流動的比對,則與經典網管流範例比對。本研究的計算結果與所有比對範例的結果相當吻合。應用實例有:船廠液體網管流、園區氮氣網管流及廠內散狀供氣網路。
前言
在工廠中所面臨到的管路非常複雜,除要獲知流動性質如流量、壓降等,有時甚至要獲得流動中的熱力學性質,如比容、溫度等。因此需要數學建模做科學計算。常見的流體管路網可概略分為:中島型網管流如 圖1及樹枝狀網管流如 圖2。管路網因有流體元件如馬達、閥等及流體流動,會造成壓能損耗,因此壓力是管路空間的函數。若考慮不穩定態流動,壓力也是時間的函數;若又是絕熱流動,亦會造成溫度隨時間在變動。這些複雜現象必須藉由物理守恆原理來了解。
圖1、中島型網管流

圖2、樹枝狀網管流

在解網管流的流量與壓力時,傳統採用引進「回路作法」[1, 2]。若方程式數目與求解變數數目不相等,就要創造虛擬回路,虛擬回路的選定並不是唯一。對於數千個節點,乃至於數萬個監控節點,虛擬回路的選定,將造成人力及時間的沉重負擔,這將留於個案研究。
本研究提出壓力與質量流率的關係式,說明質量流率可以壓力差表達,進而在各個節點上滿足質量守恆,用以替代回路選定的計算方法。所使用的方程式是控制體積型式的質量方程式及動量方程式及全能方程式(熱力學第一定理)[4, 5]。
由於工業上網管流體的輸送大抵要求流速必須小於某個特定值,通常都是遠遠小於聲速值(聲音在流體中的速度值);例如氣體聲速在常溫時,約為每秒330公尺,因此大部分的限制都在每秒100公尺以下,而科學園區的限制更為嚴格,必須每秒25公尺[3]。流體流動會導引噪音,基於法規對噪音減少的要求,這些限制的考量是必要地。在馬赫數(Mach number)小於0.3,可視流體在流動時為不可壓縮流動。在不考慮水錘現象[1]時,為方便及簡化計算,假設流體元件不堆積質量。
數學模型
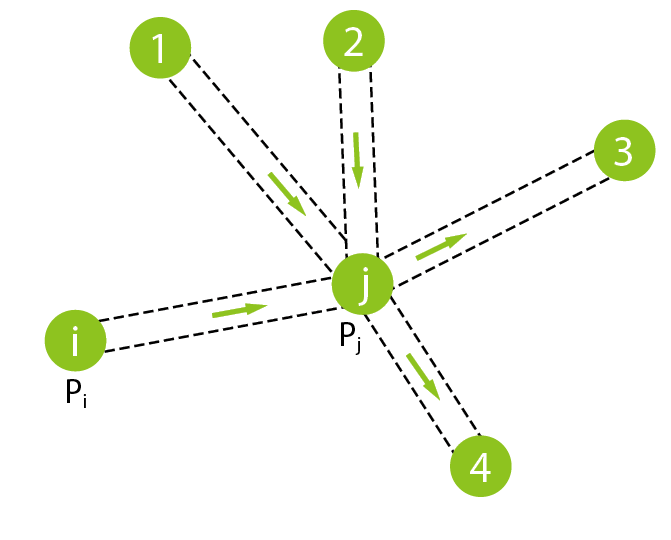
由於園區限制流體流速,必須每秒25公尺[3]以下,所以在此條件下,流體流動可視為不可壓縮,且進一步地假設流體元件不堆積質量。所以,在某個時間,管子的任一截面的質量流率相等,但卻可隨時間變動。這套理論在流體力學裡,有個名稱:Rigid Water Column Theory[1]。這裡有個重要假設,就是在處理非穩定態時,所有的流體元件,諸如管子、閥件及加壓幫浦等,都視為剛體,不可變形,也就是不考慮水鎚現象[1] 。對 圖3,由熱力學基本公式[4]或輸送現象[5],可導出質量守恆式(1)及動量守恆式(2)及全能守恆式(3)
圖3、管子流(虛線是控制體積)
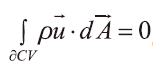 .................質量守恆式(1)
.................質量守恆式(1)
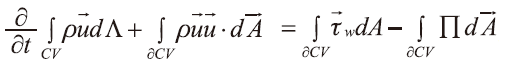 ......................動量守恆式(2)
......................動量守恆式(2)
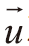 為速度向量,
為速度向量,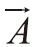 為面向量。方程式(3)僅用在絕熱及不做軸功的非穩定態氣體網管流。
為面向量。方程式(3)僅用在絕熱及不做軸功的非穩定態氣體網管流。
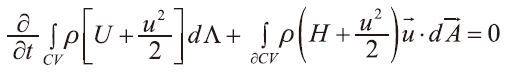 ....................全能守恆式(3)
....................全能守恆式(3)
其中CV為控制體積的勢力範圍,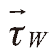 為每單位面積上的流動摩擦阻力,可表達為
為每單位面積上的流動摩擦阻力,可表達為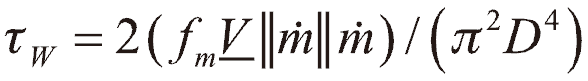 [5],ṁ 為質量流率,ƒm是摩擦因子,V為比容。Õ稱為廣義的壓力,Ⅱ ≡ P+ρgZ,ρ為密度,Z為高度,g為重力加速度大小;對氣體的網管流動,ρgZ經常被忽略。倘流體由節點 i 流向節點 j,式(2)離散展開,採用隱式法[6]可化為壓力驅動的方程式(4)
[5],ṁ 為質量流率,ƒm是摩擦因子,V為比容。Õ稱為廣義的壓力,Ⅱ ≡ P+ρgZ,ρ為密度,Z為高度,g為重力加速度大小;對氣體的網管流動,ρgZ經常被忽略。倘流體由節點 i 流向節點 j,式(2)離散展開,採用隱式法[6]可化為壓力驅動的方程式(4)
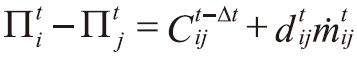 .................方程式(4)
.................方程式(4)
Ⅱi - Ⅱj > 0 代表流體由節點 i 流到節點 j,質量流率 ṁij 其值為正;據此,質量流率可用壓差直接表達。為簡潔文章內容,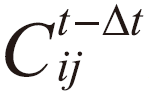 及
及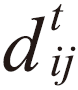 請自行推演。其中:
請自行推演。其中:
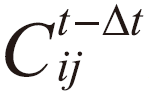 為
為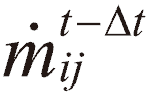 及時間步長Δt的函數。
及時間步長Δt的函數。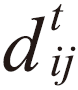 為Lij + Leq、
為Lij + Leq、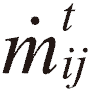 、ƒm、V及Δt的函數。
、ƒm、V及Δt的函數。- ƒm是摩擦因子,定義為[1]:ƒm = 8 [( 8 / Re )12 + 1 / ( A+B )1.5]1/12
其中:

- Re為流體流動的雷諾數,
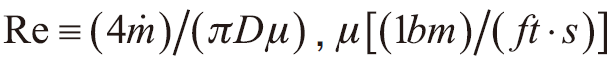 為流體流動的動力黏滯係數 (dynamic viscosity),ε 為管子粗糙度,單位是長度。
為流體流動的動力黏滯係數 (dynamic viscosity),ε 為管子粗糙度,單位是長度。 - ⟨V⟩是流體的平均比容,本研究採⟨V⟩ = ( Vi + Vj )/2,Lij > 0及 Dij > 0 則分別表示節點 i 與節點 j 的管長與管內徑。
- 當流體經過管子兩端接口的流體元件時,會有壓降損耗,常使用下兩種表達方式,一個是k,稱為管件損耗係數;另一個是Leq,稱為相當損耗長度。其物理定義分別為:ΔⅡ = κ[ ρu2/2 ],ΔⅡ = Leq[ ƒm ρu2/2D ]。常用流體元件的相當損耗長度可參考[5]。
若氣體在網管間流動為絕熱過程,須要引用全能定理及狀態方程式[4]。本研究選用PR (Peng-Robison)狀態方程式[4]。若為穩定態模擬,則式(4)中, Cij = 0且dij中有Δt項者為0。由於Excel VBA是目前最為各管理階層及工程人員所廣泛使用,因此本研究的程式乃以VBA撰寫,在Excel上讀取及呈現結果。
求解演算法
- 有( t-Δt )的熱力學及流動資訊,計算式(4)中的
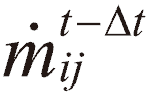 及
及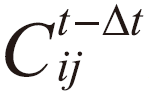 。
。 - 計算式(4)中的
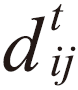 。
。 - 解式(1)及引入邊界條件,即
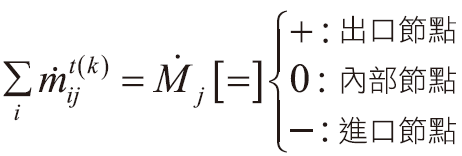 ,其中 Ṁj 為節點 j 的「淨」質量流率。
,其中 Ṁj 為節點 j 的「淨」質量流率。 - 得有所有節點
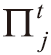 ,代入方程式(4),得有:
,代入方程式(4),得有: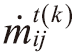 ,k 為在時間 t 時,第 k 次疊代計算。有
,k 為在時間 t 時,第 k 次疊代計算。有 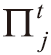 就可有
就可有 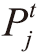 。
。 - 若為等溫流動,則每一節點有P及T,透過PR狀態方程式,可有比容V。再回到步驟(2),如此疊代計算,乃至各節點壓力全部收斂在規定的誤差範圍內,才完成時間 t 的所有計算。
- 若為絕熱流動,解方程式(3),得有所有節點上的H。節點上有H及壓力P,可求出節點的溫度T 及比容V。
- 再回到步驟(2),如此疊代計算,乃至各節點壓力P及比容V全部收斂在規定的誤差範圍內,才完成時間 t 的所有計算。
- 將 t 的資訊取代( t-Δt )的資訊,回到步驟(1),做下個時間的計算。
範例
例1 幫浦加壓管網流[2]
考慮如 圖4之水管網路。假設25℃的水,在幫浦出口處壓力是 16bar,管路末端是接收容器,曝露在大氣中。所有內管徑均為6.0603吋。其他資訊分別在 圖4。
圖4、幫浦加壓管網流概念圖
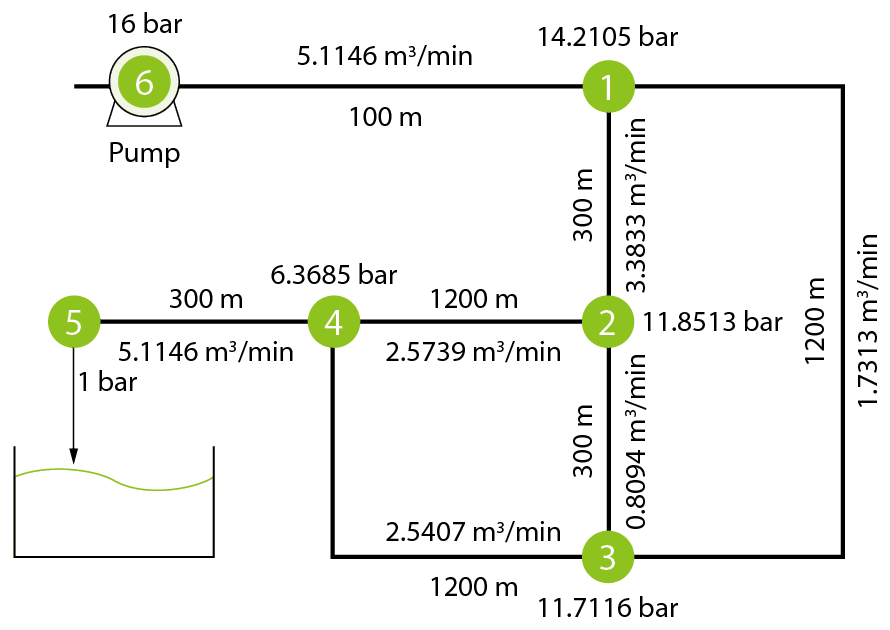
粗糙度為1.81×10-2吋。摩擦係數採用下式[2]。
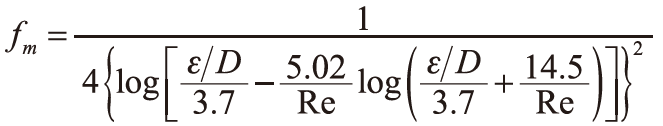
計算各點的壓力及各管路的流量。 表1為輸入必須資料,計算結果如 圖4。所得結果與給定的答案[2]完全相同,不再列出。
|
總節點數 |
至多疊帶次數 |
誤差 |
黏滯度 |
比容 |
粗糙度 |
|---|---|---|---|---|---|
|
psia |
lbm/ft/s |
ft3/lbm |
in |
||
|
6 |
100 |
1.0×10-6 |
5.9805×10-4 |
1.6065×10-2 |
1.81×10-2 |
例2 船艙內消防系統
如 圖5所示。PDMS為英國AVEVA公司發展的CAD軟體,將傳統的CAD-2D發展成3D,並結合虛擬實境,在園區稱作CAD5D,非常容易上手。
圖5、船艙內消防系統PDMS 圖
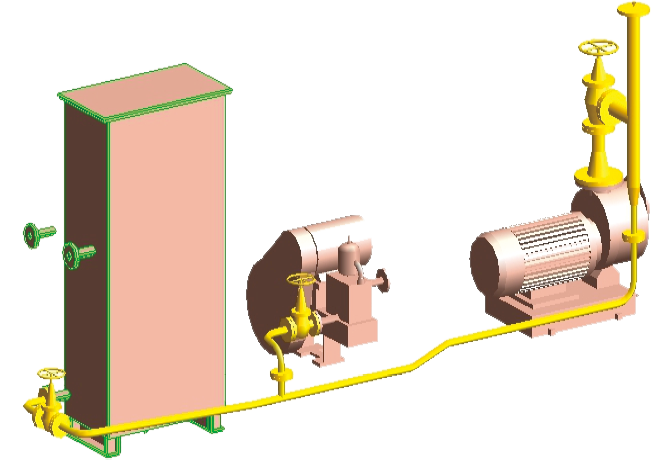
這是歐洲號稱第一名的工程畫圖軟體。由PDMS可以很容易將檔案轉為2D平面示意 圖6,這可藉由轉檔程式進行。
圖6、船艙內2D 消防系統平面示意圖

管子兩端的流體元件(節點)可直接由PDMS下載成為Excel格式,本研究所發展的程式即可立刻使用。流體物性及流動性質參數如 表2。本研究計算僅提供出口流量結果。在 圖6,編號為15及5號節點,設定為進口,壓力設為8.18bar及10bar。出口編號為6及25的節點,壓力經由調壓閥設定為4.5及5bar。穩定態結果列於 表3供參考。
|
總節點數 |
至多疊帶次數 |
誤差 |
黏滯度 |
比容 |
粗糙度 |
|---|---|---|---|---|---|
|
Nodes |
Itmax |
eps |
lbm/ft/s |
ft3/lbm |
in |
|
27 |
15 |
1.00E-06 |
6.7197E-04 |
0.0160 |
4.61E-04 |
|
出口節點 |
壓力 |
節點1 |
節點2 |
直徑 |
質量流率 |
體積流率 |
速度大小 |
|---|---|---|---|---|---|---|---|
|
編號 |
bar |
編號 |
編號 |
in |
kg/min |
m3/hr |
m/s |
|
6 |
4.5 |
7 |
6 |
0.764 |
383.5133 |
23.0108 |
21.6115 |
|
25 |
5 |
24 |
25 |
0.764 |
76.6947 |
4.6017 |
4.3219 |
例3 具有週期振動的加壓幫浦
與例2完全相同,但做動態模擬。假設幫浦出口壓力為下述值:
P節點5 = 10.0 x [ 1+0.13 x sin( 7 x t ) ][ bar ]
P節點15 = 8.18 x [ 1-0.1 x sin( 13 x t ) ][ bar ]
則結果呈現在 圖7供參考。當流體流出,質量流率為正。
圖7、動態示意圖
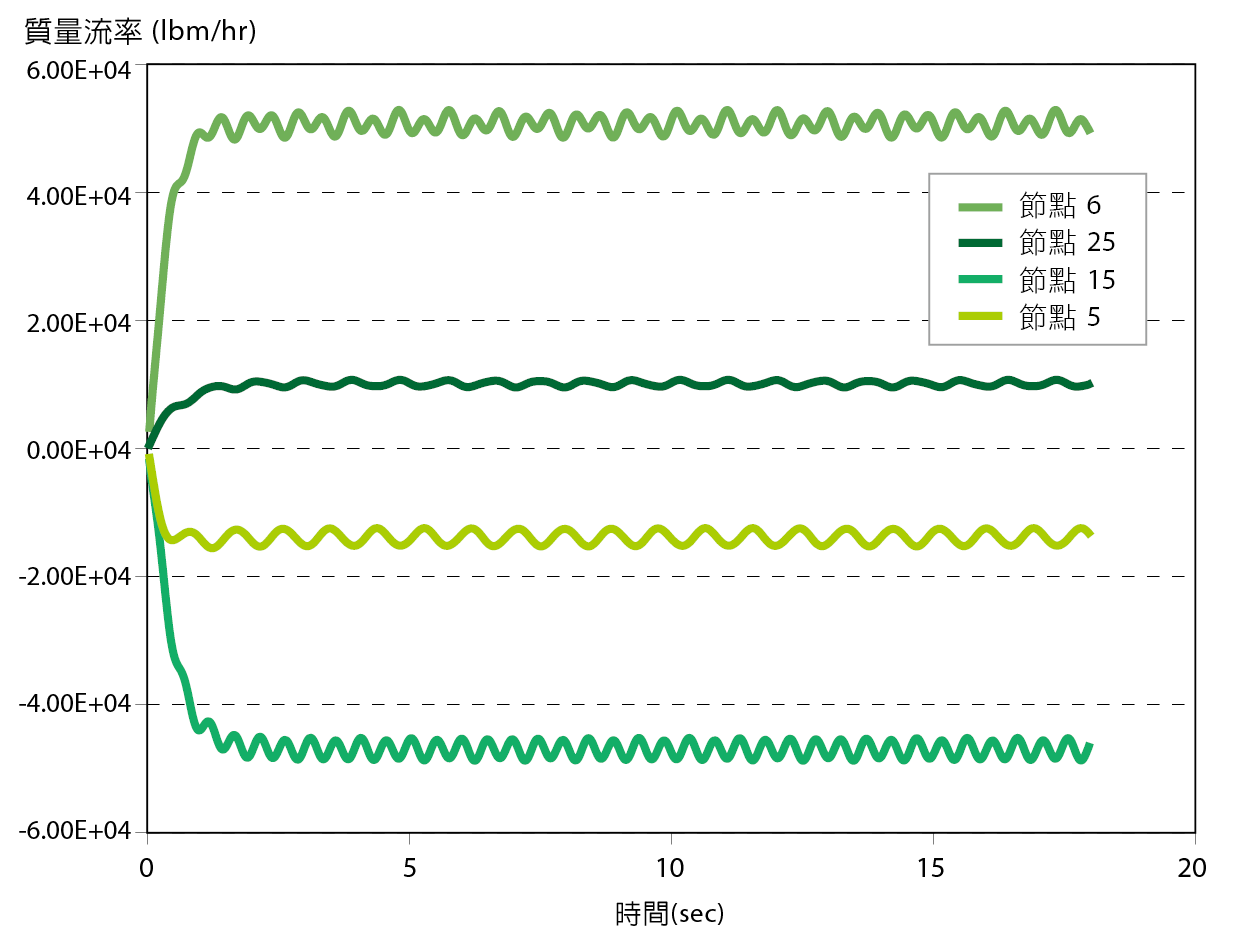
例4 氣體單直管流[7]
如 圖8,氮氣在直徑為0.75吋,長100公尺的單支管流動,進口壓力為10atm,流量為60kg/hr,求出口溫度、比容、速度及壓力。在比對例子中[7],是將溫度及比容做為變數,再透過PR狀態方程式將壓力反推出來,因此進口壓力將不再是10atm,透過PR成為10.0013atm;顯然,比對例本身就有小數第3位的誤差。除溫度外,其餘比對都接近。在出口處,本模式溫度為297.7606K,比對例為297.9610K。計算結果如 表4。
圖8、氣體單直管流

|
節點比容[m3/kg] |
節點壓力[psia] |
節點溫度[K] |
中點速率[m/Sec] |
||||||
|---|---|---|---|---|---|---|---|---|---|
|
位置[m] |
本模式 |
比對例 |
本模式 |
比對例 |
本模式 |
比對例 |
比較點 |
本模式 |
比對例 |
|
0.0000 |
0.0869 |
0.0870 |
146.9598 |
146.9796 |
298.0000 |
298.0000 |
5.0000 |
5.0861 |
5.0887 |
|
10.0000 |
0.0870 |
0.0871 |
146.7393 |
146.7561 |
297.9763 |
297.9961 |
15.0000 |
5.0934 |
5.0964 |
|
20.0000 |
0.0872 |
0.0872 |
146.5185 |
146.5323 |
297.9525 |
297.9923 |
25.0000 |
5.1007 |
5.1041 |
|
30.0000 |
0.0873 |
0.0874 |
146.2974 |
146.3082 |
297.9286 |
297.9884 |
35.0000 |
5.1080 |
5.1119 |
|
40.0000 |
0.0874 |
0.0875 |
146.0760 |
146.0837 |
297.9047 |
297.9845 |
45.0000 |
5.1154 |
5.1198 |
|
50.0000 |
0.0875 |
0.0876 |
145.8543 |
145.8588 |
297.8808 |
297.9806 |
55.0000 |
5.1228 |
5.1276 |
|
60.0000 |
0.0877 |
0.0878 |
145.6322 |
145.6336 |
297.8568 |
297.9767 |
65.0000 |
5.1302 |
5.1355 |
|
70.0000 |
0.0878 |
0.0879 |
145.4099 |
145.4081 |
297.8328 |
297.9728 |
75.0000 |
5.1376 |
5.1435 |
|
80.0000 |
0.0879 |
0.0880 |
145.1872 |
145.1822 |
297.8088 |
297.9689 |
85.0000 |
5.1451 |
5.1514 |
|
90.0000 |
0.0881 |
0.0882 |
144.9641 |
144.9560 |
297.7847 |
297.9649 |
95.0000 |
5.1527 |
5.1595 |
|
100.000 |
0.0882 |
0.0883 |
144.7408 |
144.7294 |
297.7606 |
297.9610 |
|
|
|
例5 園區網管流
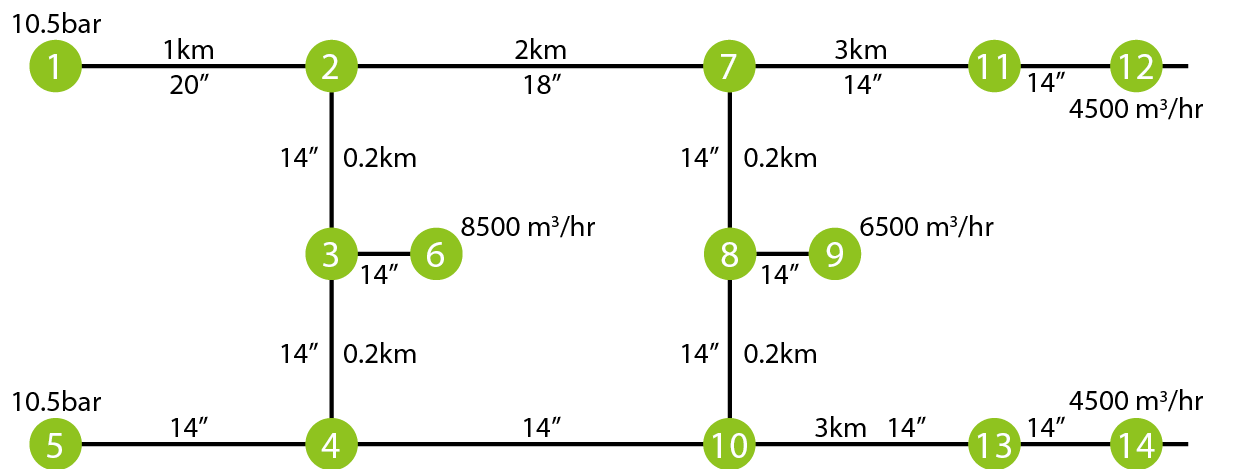
進入廠房前,戶外地下配管圖概念如 圖9。由於是地下配管,可視流動為絕熱過程。此地下配管,年代久遠,節點間的流體元件,諸如接頭及彎頭等已不可考,為方便及簡單計,相當損耗長度以管長的十分之一計算。模擬結果列於 表5供參考。
圖9、園區網管流
|
出口節點 |
壓力 |
節點1 |
節點2 |
直徑 |
質量流率 |
體積流率 |
出口速度 |
|---|---|---|---|---|---|---|---|
|
編號 |
bar |
編號 |
編號 |
in |
kg/min |
m3/hr |
m/s |
|
6 |
9.8513 |
3 |
6 |
14.00 |
1602.50 |
85000.131 |
23.95 |
|
9 |
9.1065 |
8 |
9 |
14.00 |
1225.44 |
65000.105 |
19.75 |
|
12 |
8.2779 |
11 |
12 |
14.00 |
848.39 |
45000.290 |
14.98 |
|
14 |
8.1780 |
13 |
14 |
14.00 |
848.39 |
45000.255 |
15.16 |
例6 廠內特氣散狀網管流
某一特氣,裝置在鋼瓶內,為氣液兩相。臨界溫度為TC=459K,臨界壓力為PC=45.9bar,偏心因子為ω=0.09855。其供應氣體給3個機台使用,為使壓力在鋼瓶內在供氣時不降壓,因此源源不斷地對液相加熱,使其溫度維持在293K時,鋼瓶內的飽和蒸氣壓為19.5038psia。主管路管徑3/8吋,長度約200m且約有10個彎頭,二次配管路管徑1/4吋,長度約30m且約有5個彎頭,管子粗糙度為10×10-5in。出口3氣體用量為0.12m3/hr,出口4及出口5用量為0.001m3/hr。由於並未提供CAD圖,無法畫彎頭節點,只用進出口及VMB (Valve Manifold Board),做為概念計算節點;將彎頭損失壓能轉換為損耗相當長度,一併計算。假設管路披覆著絕熱材質,可視流動為絕熱過程。想知道出口壓力及溫度,計算結果達穩定態壓力 圖10及溫度 圖11。由於節點2到節點4,與節點2到節點5的流動條件相同,幾何條件相同,所以在 圖11中,溫度曲線重疊。 圖11為動態示意圖,一開始排氣,節點3的排量遠大於節點4及節點5的排放量,所以節點3溫度,在初期溫度降較多,逐漸氣體補充上來,溫降就是靠摩擦損耗造成。逐漸地,節點3的出口溫度高於節點4及節點5的出口溫度,是因為由節點2到3的流動的摩擦係數遠小於由節點2到4或5的摩擦係數,壓能損耗較少,所以溫度較高。
圖10、廠內特氣網管流概念圖
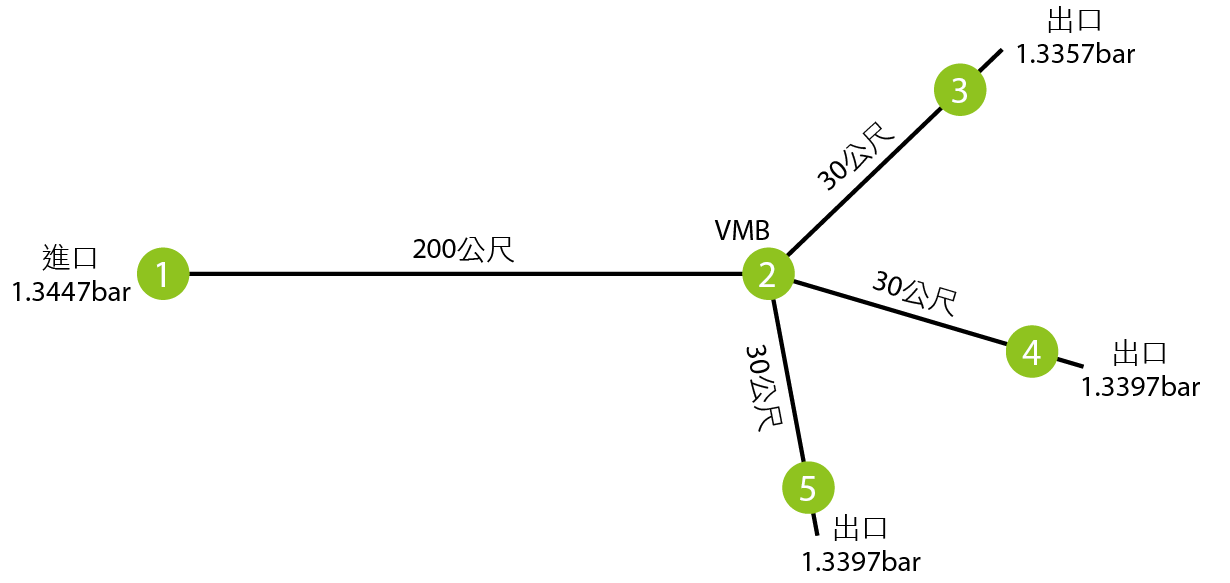
圖11、動態示意圖
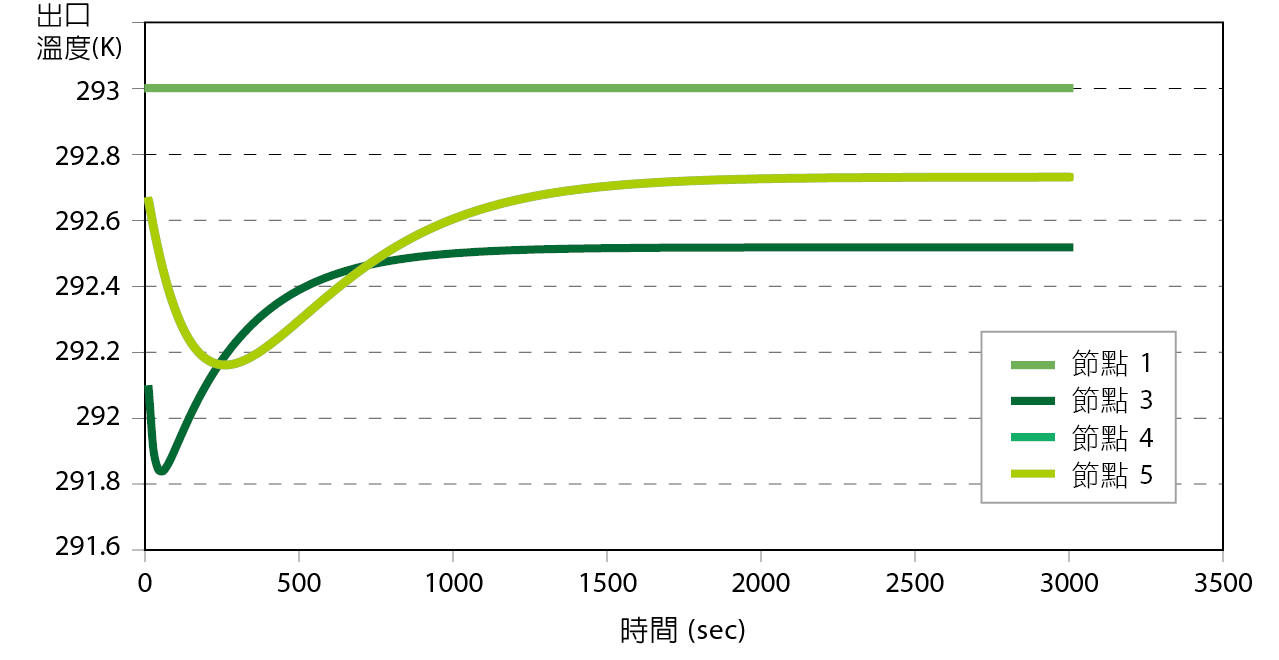
圖12、竹科十二廠六期液體管路分流

結論
本研究:
- 只需給定進出口壓力或流量,不用給回路,即可迅速得有資訊。注意:由於壓力是相對關係,至少要有一節點給定壓力。
- 對於穩定態、非穩定態、等溫與絕熱過程,都有說明計算方式。
- 液體網管流與經典範例比對,見例1,計算結果完全吻合。
- 氣體網管流與直管範例,做絕熱過程的比對,見例4,計算結果大致符合,僅溫度略有差異。本案例應較正確,其理由已在例4中說明。
- 液體網管流與實際案例比對,見例2,亦符合船公司觀察數據。
- 無論液體或氣體網管流的計算,當穩定態達到時,用穩定態算法或非穩定態算法,其結果完全一樣;如例3與例6。
- 無論消防水管路,空調管路及廢氣處理管路,廠內、外網管流都可藉本研究提出的數學模式來做設計,以確保在施工前所有的規劃都符合需求。
- 大數據時代的來臨及全世界都在提升自己的工業能力,以達所謂的工業4.0或更高值。本研究的計算,可與監控實錄數值做動態比對,見例3與例6。在PDMS上,當指標在螢幕上移到那,就會呈現所有流動性值及熱力學資料,當實際值與計算值有差10%(假設值),就會發出警告聲,提醒監控人員可能有異常,透過虛擬實境,找到可能的地方位置進行檢修,達成所謂的「防禦性遠端監控」,可大幅降低人事的作業並節省時間及財務的支出。
參考文獻
- Hodge BK, Analysis and Design of Energy Systems, 2nd edition, Prentice Hall, New Jersey, 1990.
- Cutlip MB and Shacham M, Problem Solving in Chemical Engineering with Numerical Methods, Prentice Hall, New Jersey, 1999.
- 顏登通,高科技廠務,全華,2011.
- Smith JM and Ness HCV, Introduc-tion to Chemical Engineering Ther-modynamics, 6th McGraw Hill, New York, 1996.
- Welty JR, Rorrer GL and Foster DG, Fundamentals of Momentum Heat and Mass Transfer, Wiley, New Jersey, 2015.
- Burden RL and Faires JD, Numerical Analysis, Thomson Brooks/Coile, 2005.
- Balzhiser RE, Samuels MR and Eliassen JD, Chemical Engineering Thermodynamics, Prentice Hall, New Jersey, 1972.


留言(0)